Well, well, well…

Look who decided to show up – the end of the year. Entirely unexpected and completely unforeseeable, bringing with it a strange but satisfying mix of chaos and comfort. Somehow we continue to find ourselves in this showdown again and again – 2 blog posts down, 1 to go.

Looking at date stamps, at least I’m late right on time.

As in previous years, this year’s final blog post is brought to you by the mantra: “Write what you know.” My research interests revolve around correlated data and randomized controlled trials. This includes handling of multiple primary endpoints or longitudinal endpoints in randomized controlled trials (RCTs), in particular their implications in the design and analysis of cluster randomized trials.

🌈 ⭐ 🌈 ⭐ 🌈 ⭐

On this episode of Statisticelle, we will explore the nuances of cluster randomized trials featuring a single endpoint. Freely accessible data from a real cluster randomized trial will be used to demonstrate the analysis of individual-level outcomes using linear mixed models and the nlme library in R.

🌈 ⭐ 🌈 ⭐ 🌈 ⭐

Features of cluster randomized trials

Most of us are familiar with individually randomized trials, what we may think of as the “traditional RCT,” but less so with cluster randomized trials. In a (parallel two-arm) individually randomized trial, individuals are randomly assigned to receive either the (experimental) intervention or a control, such as a placebo. Individuals hopefully receive their assigned intervention, and are followed forward in time to record outcomes of interest. Randomization helps ensure that observed, and perhaps more importantly, unobserved characteristics such as age and sex are “balanced,” or similar between arms prior to starting treatment. It also prevents other biases and provides a basis for inference, allowing us to estimate unbiased treatment effects by comparing outcomes between arms.

In cluster randomized trials, groups of individuals are instead randomly allocated to receive active treatment or a control. Common examples of clusters include schools, clinics, and families. Sometimes research interest lies in the impact of an intervention on the clusters themselves. For example, does a new policy (intervention) improve county (cluster) crime rates? In this case, use of cluster randomization is the obvious choice. In clinical settings, research interest often lies in the impact on individuals. For example, if clinics (clusters) provide referral to support services (intervention) in addition to standard of care, do patient outcomes improve? In this case, cluster randomization introduces statistical complexities not present with individual randomization, and requires justification. For example, all patients at the same clinic (cluster) receive the same intervention, which may mitigate bias arising from treatment contamination or an inability to blind interventions.

Side note 1: Individual-level analyses can be used to assess cluster-level effects, and cluster-level analyses can be used to assess individual-level effects. This is outside the scope of this introductory blog post. Check out this interesting paper on estimands (and informative cluster sizes) in cluster randomized trials to learn more.

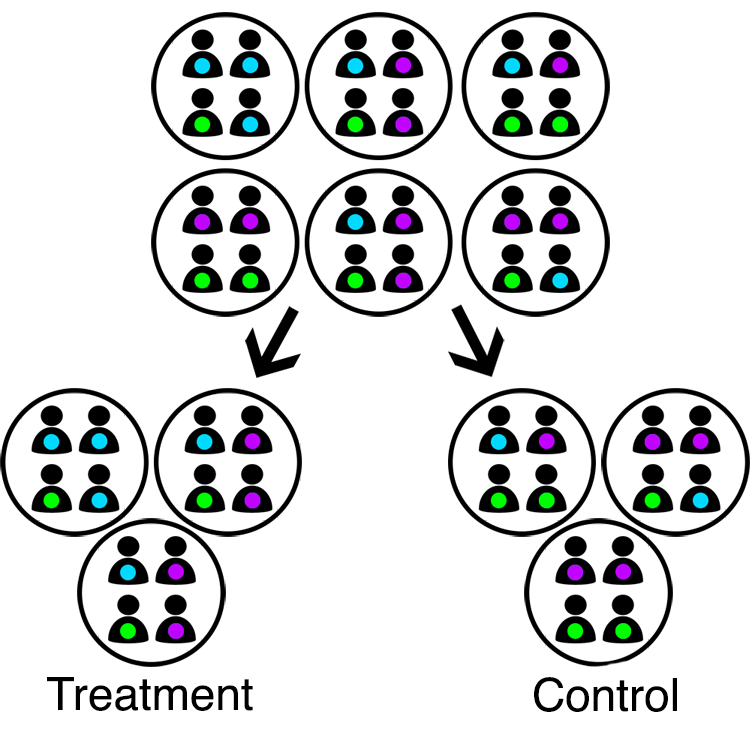
Cluster randomization.

The primary challenge of cluster randomized trials is that the unit of randomization (clusters) is not equal to the unit of analysis (individuals). Clusters are independent as a result of randomization, but individuals within the same cluster are not due to factors like shared environment. Correlation between individuals within the same cluster is referred to as “intracluster correlation” (ICC). The presence of a positive ICC suggests individuals in cluster randomized trials contribute less unique information than individuals in traditional RCTs. The larger the clusters and/or the larger the ICC, the less efficient the cluster randomized trial. The ICC must be accounted for in both design and analysis, else sample sizes and variances will be underestimated.

Balance is also a concern for cluster randomized trials. With large enough sample sizes, randomization helps ensure balance among the units of randomization. This means that cluster-level traits may be balanced, but not necessarily individual-level traits. Even so, few clusters are often randomized, e.g., due to their size (think about randomizing entire hospitals or schools)! Use of statistical methods which permit adjustment for both individual- and cluster-level traits can help combat imbalance (👀 multi-level or mixed models 👀).

Side note 2: The sample size required by a cluster randomized trial, $N_{C}$ is equal to the sample size required by an analogous individually randomized trial, $N_{I}$ , multiplied by a design effect:

(1) $\begin{equation*} N_{C} = N_{I} \left[ 1 + (m-1)~ \rho \right] \end{equation*}$

where $m$ represents cluster size and $\rho$ represents the ICC. From this relationship, it is easy to see how increasing cluster size or the ICC even slightly can result in significant increases in sample size.

Correlation structures

Before we jump into model fitting, let’s think about the correlation patterns or structures induced by cluster randomization. All clusters are independent due to randomization. Individuals are thus not correlated between-cluster, but are correlated within-cluster due to intracluster correlation, as discussed.

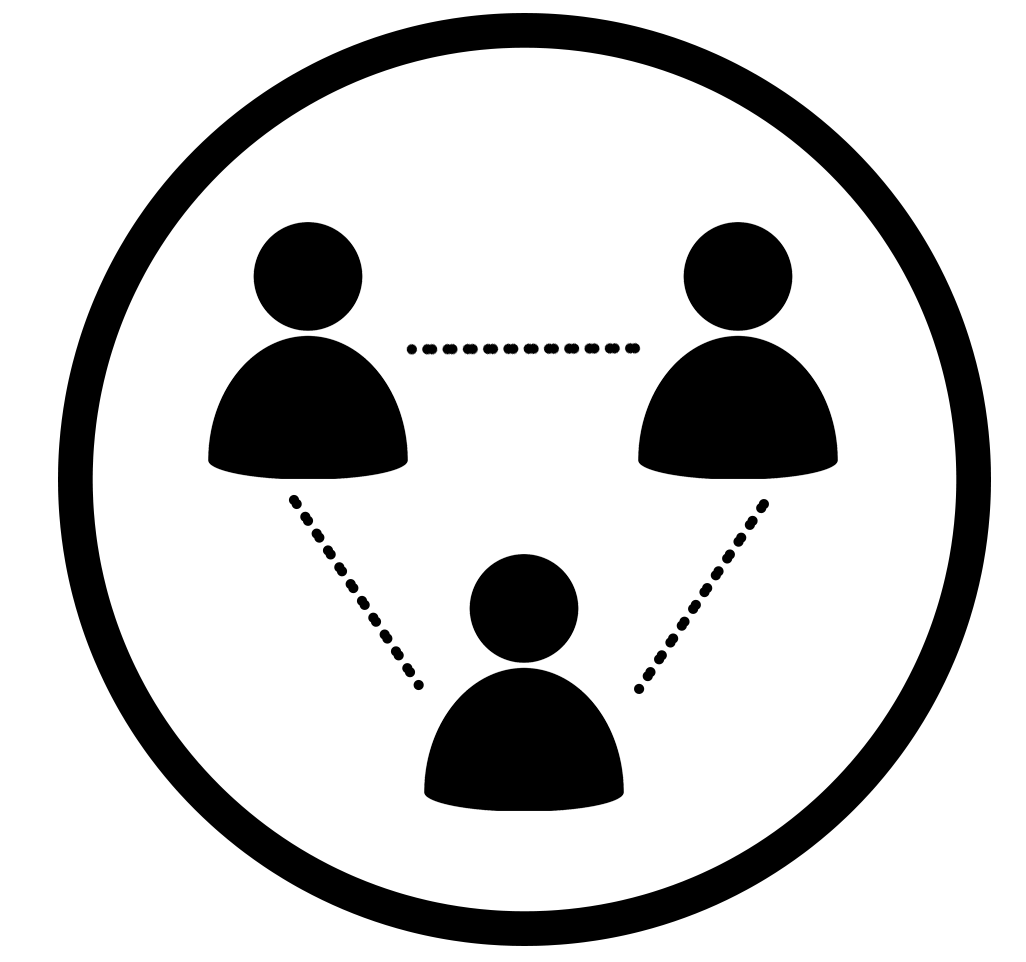
Intracluster correlation.

We typically assume that intracluster correlation is the same for any pair of individuals within a cluster, across all clusters. These assumptions result in what we call an “exchangeable” correlation matrix.

(2) $\begin{equation*} \pmb{R} = \left[\begin{matrix} 1 & \rho & \rho \\ \rho & 1 & \rho \\ \rho & \rho & 1 \end{matrix}\right] \end{equation*}$

Exchangeable correlation matrix for a cluster containing 3 individuals, where $\rho$=ICC.

Side note 3: The assumption that clusters are independent, or that individuals are independent between-cluster, can be violated. For example, if students at one school are friends with students at another school within the trial. This is referred to as “interference,” and can be mitigated by recruiting schools that are in different catchment areas or towns, for example.

Random intercept model

Cluster randomized trials are commonly analyzed using linear mixed models (LMMs), also known as multi-level models. In particular, random intercept models. Let $Y_{ij\ell}$ represent the response of the $\ell^{th}$ individual within the $j^{th}$ cluster in the $i^{th}$ arm. The form of the random intercept model is then as follows,

(3) $\begin{equation*} Y_{ij\ell} ~|~ T_{ij} = (\beta_0 + \beta_1 \text{T}_{ij} + \varepsilon_{ij\ell}) + \alpha_{ij} \end{equation*}$

where:

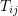$T_{ij}$ is an arm indicator equal to 1 if 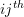$ij^{th}$ cluster randomized to active intervention and 0 if control,
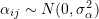$\alpha_{ij} \sim N(0, \sigma^{2}_{\alpha})$ represents the cluster-specific random intercept shared by all members the 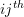$ij^{th}$ cluster, and
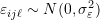$\varepsilon_{ij\ell} \sim N(0, \sigma^{2}_{\varepsilon})$ represents the error or residual specific to the 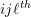$ij\ell^{th}$ individual-level response, and
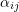$\alpha_{ij}$ is assumed to be independent of $\varepsilon_{ij\ell}$ .

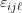The bracketed part of the random intercept model resembles your traditional linear regression model. Coefficient $\beta_1$ represents the mean response within the control arm, $\bar{Y}_{0\cdot\cdot}$ , and $\beta_1$ represents the mean difference between arms, $\bar{Y}_{1\cdot\cdot} - \bar{Y}_{0\cdot\cdot}$ . By including random intercept $\alpha_{ij}$ , we induce the exchangeable correlation structure discussed in the previous section.

Side note 4: With few clusters (less than 30 or 40), linear mixed models, as well as alternative GEEs, may result in inflated type I error rates. There are a number of small-sample adjustments that can help correct this.

By model definition, the total variation in the individual-level responses is $\text{V}[Y_{ij\ell}] = \sigma^{2}_{\alpha} + \sigma^{2}_{\varepsilon}$ , where $\sigma^{2}_{\alpha}$ measures variation between-clusters and $\sigma^{2}_{\varepsilon}$ variation between-individuals. In addition to being defined as the correlation between members of the same cluster, the intracluster correlation can also be constructed as the proportion of total variation explained by differences between clusters. Formally,

(4) $\begin{equation*} \rho = \frac{\sigma^{2}_{\alpha}}{\sigma^{2}_{\alpha} + \sigma^{2}_{\varepsilon}} = \frac{\text{Between-cluster variance}}{\text{Total variance}}. \end{equation*}$

Side note 5: Intracluster correlation can be negative, in which case this definition of the ICC is problematic. This is somewhat uncommon in clinical settings, and thus not the focus here. However, this may occur when individuals within the same cluster compete for resources. One example is competition between litter mates, another is competition for speaking time during group therapy.

We will use data from a real cluster randomized trial for demonstration, downloadable in different formats from the Harvard Dataverse (click “Access File” to download). This dataset, also used as an example in Hayes’ & Moulton’s textbook, corresponds to a two-arm cluster randomized trial that investigated whether an experimental sex education programme, Sexual Health and Relationships: Safe, Happy and Responsible (SHARE), reduced unsafe sex among students in Scotland versus existing sex education (control). Further detail about the trial may be found within,

Wight D, Raab GM, Henderson M et al. Limits of teacher delivered sex education: interim behavioural outcomes from randomised trial. BMJ 2002; 324: 1430-1435. doi: 10.1136/bmj.324.7351.1430

SHARE <- read.table('share.tab', sep='\t', header=T)
str(SHARE)

## 'data.frame':	5854 obs. of  8 variables:
##  $ school: int  1 1 1 1 1 1 1 1 1 1 ...
##  $ sex   : int  2 2 2 2 2 1 1 1 1 2 ...
##  $ arm   : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ scpar : int  31 31 99 20 20 20 40 31 31 20 ...
##  $ debut : int  1 1 0 0 1 0 0 0 0 0 ...
##  $ regret: int  NA 0 NA NA NA NA NA NA NA NA ...
##  $ kscore: int  3 5 4 4 6 8 5 6 2 4 ...
##  $ idno  : num  1 2 3 4 5 6 7 8 9 10 ...

Schools were randomized as clusters (school) to deliver the SHARE curriculum (arm==1) or not (arm==0). At baseline, the sex of each student (sex) was captured. At follow-up, student sexual health knowledge was assessed by a knowledge score (kscore), ranging from -8 (least knowledgable) to +8 (most knowledge). We will focus on these four variables.

# Subset rows and columns to complete cases of 4 variables
SHARE <- SHARE[,c('arm', 'school', 'sex', 'kscore')]
SHARE <- SHARE[complete.cases(SHARE),]

In our subsetted data, we see 25 schools randomized, 12 to control and 13 to SHARE, corresponding to 5,501 total students, 2,812 at control schools and 2,689 at SHARE schools. Even though we have a TON of students, we have relatively few clusters! There appears to be slight differences between arms in the proportion of female students (p_female) at baseline and mean knowledge score (m_kscore) at follow-up.

library(tidyverse)

SHARE %>%
  group_by(arm) %>%
  summarize(n_schools  = n_distinct(school),
            n_students = n(),
            p_female   = sum(sex-1)/n(),
            m_kscore   = mean(kscore))

## # A tibble: 2 × 5
##     arm n_schools n_students p_female m_kscore
##   <int>     <int>      <int>    <dbl>    <dbl>
## 1     0        12       2812    0.522     4.15
## 2     1        13       2689    0.554     4.77

Side note 6: For the purposes of this post, we will assume that knowledge score can be treated as a continuous variable. However, I would personally classify this outcome as ordinal. You can check out my previous blogpost, Minor musings on measurement, to learn more about the properties of ordinal data, and debates on their handling in analysis. You could also check out this super cool, really great paper on rank-based estimation in cluster randomized trials. coughcough No bias here! coughcough

Model fitting using nlme in R

We can easily fit linear mixed models using the lme function from the nlme library in R. Alternative libraries such as lme4 in R or the PROC MIXED procedure in SAS can also be used to fit these models. There is a lot of nuance to fitting linear mixed models, such as use of REML vs. ML, etc. Defaults and functionality are likely to differ from package-to-package, and it is important to review documentation for any libraries or programs you are using for model fitting. My personal favourites are nlme and PROC MIXED, but I know others have strong opinions otherwise! So take a look to see what works best for you, particularly in more complex scenarios.

To fit our linear mixed model, we start by specifying the relationship between our outcome and intervention arm, equal to the fixed part of our model. Next, we specify a random intercept for each school (cluster) by including random=~1|school. It’s that easy!

library(nlme)
lmm <- lme(# specify: outcome~covariate relationship
           fixed=kscore~arm, 
           # specify: random intercept for each school
           random=~1|school, 
           # specify: data source
           data=SHARE)

Under Fixed effects, the estimated coefficient for arm suggests that the SHARE curriculum increased sexual health knowledge scores by an average of 0.54 points compared to the conventional curriculum. Under Random effects, we see that the estimated cluster variance (Intercept) is $\hat{\sigma}_{\alpha}^{2} = 0.393^{2} = 0.15$ and the residual variance (Residual) is $\hat{\sigma}^{2}_{\varepsilon} = 2.32^{2} = 5.38$ . Thus, the estimated intracluster correlation is $\hat{\rho} = 0.15/(0.15+5.38) = 0.027$ .

summary(lmm)

## Linear mixed-effects model fit by REML
##   Data: SHARE 
##     AIC   BIC logLik
##   24914 24940 -12453
## 
## Random effects:
##  Formula: ~1 | school
##         (Intercept) Residual
## StdDev:       0.393     2.32
## 
## Fixed effects:  kscore ~ arm 
##             Value Std.Error   DF t-value p-value
## (Intercept)  4.12     0.122 5476    33.7  0.0000
## arm          0.54     0.171   23     3.1  0.0045
##  Correlation: 
##     (Intr)
## arm -0.716
## 
## Standardized Within-Group Residuals:
##     Min      Q1     Med      Q3     Max 
## -4.6883 -0.6019  0.0652  0.6931  1.9619 
## 
## Number of Observations: 5501
## Number of Groups: 25

Side note 7: An intracluster correlation of 0.027 may seem small, but most intracluster correlations are! Small ICCs have large impacts on efficiency – so don’t ignore them!!

When we adjust for slight differences in sex between arms, we see that the treatment effect (coefficient) of arm is attenuated slightly. Notice also the difference in degrees of freedom for the covariates arm and sex. This is because arm is a cluster-level covariate and sex is an individual-level covariate.

# Fit model
lmm_adj <- lme(kscore~arm+sex, random=~1|school, data=SHARE)
summary(lmm_adj)

## Linear mixed-effects model fit by REML
##   Data: SHARE 
##     AIC   BIC logLik
##   24721 24754 -12356
## 
## Random effects:
##  Formula: ~1 | school
##         (Intercept) Residual
## StdDev:        0.41     2.27
## 
## Fixed effects:  kscore ~ arm + sex 
##             Value Std.Error   DF t-value p-value
## (Intercept) 2.785    0.1576 5475   17.67  0.0000
## arm         0.509    0.1765   23    2.88  0.0084
## sex         0.877    0.0617 5475   14.22  0.0000
##  Correlation: 
##     (Intr) arm   
## arm -0.568       
## sex -0.597 -0.011
## 
## Standardized Within-Group Residuals:
##     Min      Q1     Med      Q3     Max 
## -4.5816 -0.6154  0.0789  0.7378  2.2226 
## 
## Number of Observations: 5501
## Number of Groups: 25

Go forth and conquer!

I mean… if you think about it, individually randomized trials are a special case of cluster randomized trials, with each individual representing a cluster of size 1! I think that understanding cluster randomized trials can both help deepen understanding of conventional RCTs, and make other complex designs like stepped wedge trials and individually randomized group treatment trials more intuitive and accessible. I hope this blog post helps, even if just a teeny tiny bit.

Ta ta for now!

Literally looking forward to the New Year.

Comprehending complex designs: Cluster randomized trials

Well, well, well…

🌈 ⭐ 🌈 ⭐ 🌈 ⭐

🌈 ⭐ 🌈 ⭐ 🌈 ⭐

Features of cluster randomized trials

Correlation structures

Random intercept model

Model fitting using nlme in R

Go forth and conquer!

Ta ta for now!

Published by

Emma Davies Smith

Leave a Reply Cancel reply

Well, well, well…

🌈 ⭐ 🌈 ⭐ 🌈 ⭐

🌈 ⭐ 🌈 ⭐ 🌈 ⭐

Features of cluster randomized trials

Correlation structures

Random intercept model

A real example: SHARE

Model fitting using nlme in R

Go forth and conquer!

Ta ta for now!

Published by

Emma Davies Smith

Leave a Reply Cancel reply