Overview
In my previous blogpost, I motivated the EM algorithm in the context of estimating the parameters of a two-component Gaussian mixture density. In this case, we can write the estimators of the mixing probability, means, and variance in a nice closed form, and I demonstrated how to implement the corresponding iterative estimation procedure from scratch. Results were then compared to those obtained from the very nice R package flexmix.
However, rarely do we get such nice closed form estimators! We usually need to use numerical methods to maximize our objective function directly. In this blog post, I demonstrate how we can specify our objective function, and use the optim function in R to obtain our parameter estimates. optim has lots of options, and we will cover how to change the optimization procedure and implement restrictions on our parameter spaces.
EM for two-component Gaussian mixture
Let’s quickly recap our motivation, previously discussed in Embracing the EM algorithm: One continuous response.
We randomly sample ![]() patients from a population, and examine the empirical density of their responses. We notice two modes, and based on prior knowledge, hypothesize that the density is actually a mixture of two Gaussian densities. For example, the density centered around greater responses may correspond to “healthy” patients and the other to “ill” patients. We would like to (1) estimate the probability of belonging to each subpopulation; and (2) estimate subpopulation parameters, e.g. mean response in among the healthy and ill. But, we have a problem: we don’t know who belongs to each subpopulation. In other words, subpopulation labels are unobserved or “latent.”
patients from a population, and examine the empirical density of their responses. We notice two modes, and based on prior knowledge, hypothesize that the density is actually a mixture of two Gaussian densities. For example, the density centered around greater responses may correspond to “healthy” patients and the other to “ill” patients. We would like to (1) estimate the probability of belonging to each subpopulation; and (2) estimate subpopulation parameters, e.g. mean response in among the healthy and ill. But, we have a problem: we don’t know who belongs to each subpopulation. In other words, subpopulation labels are unobserved or “latent.”
Figure: Observed two-component Gaussian mixture density (purple), and distribution of responses among latent healthy (blue) and ill (red) patient subpopulations.
We can represent the density of the observed responses as a mixture of the subpopulation densities:
![]()
That is, individuals belong to the first subpopulation, or are distributed according to density ![]() , according to probability
, according to probability ![]() and to the second, distributed per
and to the second, distributed per ![]() , with probability
, with probability ![]() . We assume both densities are Gaussian with respective means
. We assume both densities are Gaussian with respective means ![]() and
and ![]() and variances
and variances ![]() and
and ![]() .
.
Including our “mixing probability” ![]() , the vector of all parameters is
, the vector of all parameters is ![]() . Suppose we use a traditional maximum likelihood approach to estimation, and begin by defining the marginal log-likelihood as a function of our sample of
. Suppose we use a traditional maximum likelihood approach to estimation, and begin by defining the marginal log-likelihood as a function of our sample of ![]() observed responses
observed responses ![]() :
:
![]()
While this appears simple in form, this log-likelihood can be surprisingly challenging to maximize. The EM algorithm gets around this through clever re-expression of the mixture density in terms of the observed response and a latent random variable corresponding to subpopulation membership.
Let ![]() be a random subpopulation indicator, equal to 1 if individual
be a random subpopulation indicator, equal to 1 if individual ![]() belongs to the first subpopulation (“healthy”) and 0 otherwise (“ill”). We have by definition
belongs to the first subpopulation (“healthy”) and 0 otherwise (“ill”). We have by definition ![]() and
and ![]() , which can be represented compactly as:
, which can be represented compactly as:
![]()
The joint density of ![]() and
and ![]() is then given through application of Bayes’ Theorem,
is then given through application of Bayes’ Theorem,
![]()
and using marginalization, you can check that we obtain the same form of ![]() given above.
given above.
If we observed both ![]() and
and ![]() , the complete data log-likelihood would take the form:
, the complete data log-likelihood would take the form:
![]()
The complete data log-likelihood is better behaved for at least two reasons: (1) the logarithm now acts directly on the Normal densities; and (2) the complete data log-likelihood is simply the sum of contributions from the two components. But, of course, we don’t observe the ![]() ! By taking the expectation of the complete data log-likelihood conditional on the observed
! By taking the expectation of the complete data log-likelihood conditional on the observed ![]() , we get a function no longer featuring
, we get a function no longer featuring ![]() :
:
![]()
where
![]()
and similarly, ![]() . We can maximize this function with respect to
. We can maximize this function with respect to ![]() , treating the weights
, treating the weights ![]() as fixed. But, since the weights feature the parameters, we will need to use iteration.
as fixed. But, since the weights feature the parameters, we will need to use iteration.
Formally, at the ![]() iteration, we consider the objective function:
iteration, we consider the objective function:
![]()
where
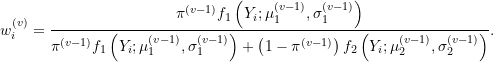
Notice that weights at the ![]() step are estimated using parameter estimates from the previous
step are estimated using parameter estimates from the previous ![]() step. The EM algorithm then proceeds as follows:
step. The EM algorithm then proceeds as follows:
- Initialize the parameter vector,
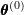 .
. - E-step: Estimate the weights
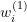 using
using 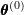 .
. - M-step: Maximize the objective function with respect to
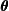 to obtain
to obtain 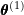 :
:
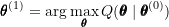
- Check for convergence in
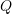 or the parameter vector. If convergence is met, stop. Else, repeat steps 2 through 4.
or the parameter vector. If convergence is met, stop. Else, repeat steps 2 through 4.
In what follows, we implement this algorithm using optim to perform our M-step!
Implementation
The EM algorithm splits things nicely into two steps, and we will follow this setup here by defining modular functions for our E-step and our M-step. But, first things first, we need to generate some data and initialize our estimates.
Data generation
For comparison, we will use exactly the same data generation process as the companion blogpost Embracing the EM algorithm: One continuous response. We set the following:
- Sample size to
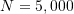 ;
; 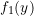 equal to
equal to 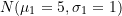 ;
;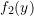 equal to
equal to 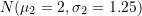 ;
;- Mixing probability equal to
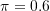 .
.
The following chunk generates data from the specified mixture by first sampling the true value of the latent class ![]() from a Bernoulli distribution. Conditional on the drawn
from a Bernoulli distribution. Conditional on the drawn ![]() , the response
, the response ![]() is generated from the corresponding Gaussian distribution.
is generated from the corresponding Gaussian distribution.
set.seed(12345)
# Simulate two-component Gaussian mixture
## Sample size
N = 5000
## Parameters for first component
mu1 <- 5; sigma1 <- 1
## Parameters for second component
mu2 <- 2; sigma2 <- 1.25
## Mixing probability
pi <- 0.6
## True parameter vector
truth <- c(pi, mu1, sigma1, mu2, sigma2)
## Sample latent class
z <- rbinom(n=N, size=1, prob=pi)
## Sample response based on latent class
y1 <- rnorm(n=sum(z==1), mean=mu1, sd=sigma1)
y2 <- rnorm(n=sum(z==0), mean=mu2, sd=sigma2)
# Combine all responses into a single vector
y <- c(y1, y2)
library(tidyverse)
## Visualize mixture distribution
qplot(x=y, geom=c('histogram')) +
labs(x='Observed response, y', y='Observed frequency') +
theme_bw()
Figure: Histogram of N=5000 responses generated from our two-component Gaussian mixture.
E-step
Given the previous iteration’s parameter estimates, the E-step estimates the weights ![]() . For simplification, I first reskin
. For simplification, I first reskin dnorm to align with the notation used here. If log=T then the log density is returned (helpful for log-likelihood).
# First density
f1 <- function(y, Mu1, Sigma1, log=F){ dnorm(y, mean=Mu1, sd=Sigma1, log=log) }
# Second density
f2 <- function(y, Mu2, Sigma2, log=F){ dnorm(y, mean=Mu2, sd=Sigma2, log=log) }
We need to pass in the data y and a vector of parameter values theta (corresponding to ![]() defined previously).
defined previously).
EStep <- function(y, theta){
# E-STEP: Estimate weights
# Extract parameter values
Pi <- theta[1]
Mu1 <- theta[2]; Sigma1 <- theta[3]
Mu2 <- theta[4]; Sigma2 <- theta[5]
# Compute numerator and denominator of weight w
Numerator <- Pi * f1(y, Mu1, Sigma1)
Denominator <- Pi * f1(y, Mu1, Sigma1) + (1-Pi) * f2(y, Mu2, Sigma2)
# Calculate and return weights W
w <- Numerator / Denominator
return(w)
}
M-step using optim
Now for the moment you’ve all been waiting for – performing the Maximization or M-step using optim!
We first need to turn our objective function (the function we want to maximize) into an R function that we can later pass to optim. The arguments of ![]() are: the data
are: the data y, the current values of the weights w, and the current parameter estimates theta.
Q <- function(y, w, theta){
# OBJECTIVE FUNCTION
# Extract parameter values
Pi <- theta[1]
Mu1 <- theta[2]; Sigma1 <- theta[3]
Mu2 <- theta[4]; Sigma2 <- theta[5]
# Calculate two terms of Q per subject (notice log=T in f)
Term1 <- w*log(Pi) + w*f1(y, Mu1, Sigma1, log=T)
Term2 <- (1-w)*log(1-Pi) + (1-w)*f2(y, Mu2, Sigma2, log=T)
# Add 'em all together and return
Q <- sum(Term1) + sum(Term2)
return(Q)
}
We wrap optim in an M-step function which requires the same arguments as ![]() . The
. The optim function will return the maximized value of ![]() and corresponding parameter estimates in a named list, so we store the results to access them. We use ‘BFGS’ as our unconstrained optimization technique (default), but there are several options available such as ‘Nelder-Mead’. See
and corresponding parameter estimates in a named list, so we store the results to access them. We use ‘BFGS’ as our unconstrained optimization technique (default), but there are several options available such as ‘Nelder-Mead’. See ?optim for more details.
MStep <- function(y, w, theta){
# M-STEP: Maximize objective function
# Specify optim arguments
maxQ <- optim(# function to optimize
fn = Q,
# initial (current) parameter values
par = theta,
# additional user specified arguments to pass to fn
y = y,
w = w,
# optimization method, see help for options
method = 'BFGS',
# optim minimizes by default, specify fnscale = -1 to maximize
control = list(fnscale = -1)
)
# Return results of maximization = (Q, theta)
results <- list(Qval=maxQ$value, theta=maxQ$par)
}
Initialization and iteration
Each step of maximizing the objective function ![]() should increase the value of the marginal log-likelihood. However, the EM algorithm is only guaranteed to find a local maxima. Thus, in general, it is quite sensitive to the choice of starting estimates. There are a lot of strategies for dealing with this, such as selecting multiple sets of initial values and retaining the set which performs best, i.e., results in the greatest likelihood. For complex models, it can also be challenging to even know how to reasonably obtain initial estimates!
should increase the value of the marginal log-likelihood. However, the EM algorithm is only guaranteed to find a local maxima. Thus, in general, it is quite sensitive to the choice of starting estimates. There are a lot of strategies for dealing with this, such as selecting multiple sets of initial values and retaining the set which performs best, i.e., results in the greatest likelihood. For complex models, it can also be challenging to even know how to reasonably obtain initial estimates!
Here, we use the k-means algorithm to cluster the data into two groups and treat predicted labels as the true value of ![]() . Within the two groups defined by
. Within the two groups defined by ![]() , we can independently obtain initial estimates of
, we can independently obtain initial estimates of ![]() and
and ![]() .
.
Q_vec <- c()
est_list <- list()
for (b in 1:1000){
# Initialize parameter values
if (b==1){
# Apply k-means with two centers
kinit <- kmeans(y, centers=2)
# Store predicted cluster labels
cluster <- kinit$cluster
# Estimate mixture probability
Pi <- sum(cluster==1)/N
# Estimate first component parameters
y1 <- y[cluster==1]
Mu1 <- mean(y1)
Sigma1 <- sd(y1)
# Estimate second component parameters
y2 <- y[cluster==2]
Mu2 <- mean(y2)
Sigma2 <- sd(y2)
# Parameter vector
theta <- c(Pi, Mu1, Sigma1, Mu2, Sigma2)
# Objective function
Qval <- Q(y, EStep(y, theta), theta)
}
else {
# E-Step
w <- EStep(y, theta)
# M-Step
M <- MStep(y, w, theta)
Qval <- M$Qval
theta <- M$theta
}
# Update log-likelihood vector and estimate list
Q_vec[b] <- Qval
est_list[[b]] <- theta
if (b > 1) { if (abs(Q_vec[b] - Q_vec[(b-1)]) < 0.01) break }
}
rbind(c('True values:', truth),
c('Inital estimate:', round(est_list[[1]], 3)),
c('Best estimate:', round(est_list[[length(Q_vec)]], 3)))
## [,1] [,2] [,3] [,4] [,5] [,6] ## [1,] "True values:" "0.6" "5" "1" "2" "1.25" ## [2,] "Inital estimate:" "0.375" "1.756" "1.052" "5.002" "0.917" ## [3,] "Best estimate:" "0.406" "2" "1.28" "5.004" "0.979"
Ah! This is something we saw in Embracing the EM algorithm: One continuous response! Cluster or component labels are not unique. Here, the algorithm has “swapped” the component labels. That’s okay, we are smart enough to figure out which is which. However, this can be tricky for more complex problems… Constrained optimization presents one solution, discussed shortly.
rbind(c('Initial objective:', round(Q_vec[1], 3)),
c('Best objective:', round(Q_vec[length(Q_vec)], 3)),
c('No. of iterations:', length(Q_vec)))
## [,1] [,2] ## [1,] "Initial objective:" "-10586.343" ## [2,] "Best objective:" "-10909.606" ## [3,] "No. of iterations:" "87"
LL <- function(y, theta){
# Extract parameter values
Pi <- theta[1]
Mu1 <- theta[2]; Sigma1 <- theta[3]
Mu2 <- theta[4]; Sigma2 <- theta[5]
Term <- log(Pi * f1(y, Mu1, Sigma1) + (1-Pi) * f2(y, Mu2, Sigma2))
LL <- sum(Term)
return(LL)
}
plot(unlist(lapply(est_list, FUN=function(X) LL(y, X))),
type='l', xlab='Iteration', ylab='Marginal log-likelihood')
Marginal (observed) log-likelihood at each iteration of the EM algorithm.
Constrained optimization with L-BFGS-B
The previous M-step and optim procedure performed unconstrained optimization for all parameters in theta over the range ![]() . However, we often need to constrain certain parameters to fall within a given range. For example, the variances
. However, we often need to constrain certain parameters to fall within a given range. For example, the variances ![]() and
and ![]() only exist within the range
only exist within the range ![]() . Another example is correlation which is bounded within
. Another example is correlation which is bounded within ![]() .
.
By setting method = 'L-BFGS-B', we can set lower and upper constraints on the optimization of specific parameters. The following code sets bounds of ![]() for each of the
for each of the ![]() . We can also address our label problem, by restricting the range of
. We can also address our label problem, by restricting the range of ![]() to
to ![]() so the first component is forced to be properly identified. Unbounded variables have
so the first component is forced to be properly identified. Unbounded variables have lower and upper set to -Inf and Inf, respectively.
MStep2 <- function(y, w, theta){
# M-STEP: Maximize objective function
# Specify optim arguments
maxQ <- optim(# function to optimize
fn = Q,
# initial (current) parameter values
par = theta,
# additional user specified arguments to pass to fn
y = y,
w = w,
# optimization method, see help for options
method = 'L-BFGS-B',
# Bounds on Pi, Mu1, Sigma1, Mu2, Sigma2
lower = c(0.5, -Inf, 0, -Inf, 0),
upper = c(1.0, Inf, Inf, Inf, Inf),
# optim minimizes by default, specify fnscale = -1 to maximize
control = list(fnscale = -1)
)
# Return results of maximization = (Q, theta)
results <- list(Qval=maxQ$value, theta=maxQ$par)
}
Q_vec <- c()
est_list <- list()
for (b in 1:1000){
# Initialize parameter values
if (b==1){
# Apply k-means with two centers
kinit <- kmeans(y, centers=2)
# Store predicted cluster labels
cluster <- kinit$cluster
# Estimate mixture probability
Pi <- sum(cluster==1)/N
# Estimate first component parameters
y1 <- y[cluster==1]
Mu1 <- mean(y1)
Sigma1 <- sd(y1)
# Estimate second component parameters
y2 <- y[cluster==2]
Mu2 <- mean(y2)
Sigma2 <- sd(y2)
# Parameter vector
theta <- c(Pi, Mu1, Sigma1, Mu2, Sigma2)
# Objective function
Qval <- Q(y, EStep(y, theta), theta)
}
else {
# E-Step
w <- EStep(y, theta)
# M-Step
M <- MStep2(y, w, theta)
Qval <- M$Qval
theta <- M$theta
}
# Update log-likelihood vector and estimate list
Q_vec[b] <- Qval
est_list[[b]] <- theta
if (b > 1) { if (abs(Q_vec[b] - Q_vec[(b-1)]) < 0.01) break }
}
rbind(c('True values:', truth),
c('Inital estimate:', round(est_list[[1]], 3)),
c('Best estimate:', round(est_list[[length(Q_vec)]], 3)))
## [,1] [,2] [,3] [,4] [,5] [,6] ## [1,] "True values:" "0.6" "5" "1" "2" "1.25" ## [2,] "Inital estimate:" "0.625" "5.002" "0.917" "1.756" "1.052" ## [3,] "Best estimate:" "0.593" "5.006" "0.978" "2.005" "1.282"
And voila! The components are properly ordered. We don’t see a difference in the ![]() , but they aren’t problematically close to
, but they aren’t problematically close to ![]() .
.
Concluding thoughts
Motivated by a two-component Gaussian mixture, this blog post demonstrates how to maximize objective functions using R’s optim function. Unconstrained maximization using BFGS and constrained maximization using L-BFGS-B is demonstrated. There are alternative ways of performing constrained optimization, for example, by performing unconstrained optimization on a transformed parameter space (similar idea to use of a link function in generalized linear models). I’ll cover this in my next blogpost, as it gets into some neat properties of maximum likelihood estimation and optimization! Hope this is helpful.
P.S. Shoutout and thanks to Dr. Tom Chen and Ph.D. student Nick Birk for their help on related implementations.

An update:
Sooo TBH, I tried re-running the constrained optimization presented here and got awful parameter values.
This is because the initial values pointed the algorithm in the direction of pi=0.4 rather than 0.6, so pi ended up estimated on the boundary at pi=0.5, and the rest of the estimates were goofy as a result. I thought I was sooo clever too, haha!
The EM algorithm is so sensitive to initial values, it’s driving me mad! A common suggestion appears to be multi-start, i.e. using multiple start positions and then choosing the best one based on the highest likelihood within a few iterations.
Multistart just doesn’t seem satisfying to me. I wish there were a more robust, not terribly complicated way to set up the EM algorithm on the right foot.
If anyone has any thoughts, please share!