Resampling methods approximate the sampling distribution of a statistic or estimator. In essence, a sample taken from the population is treated as a population itself. A large number of new samples, or resamples, are taken from this “new population”, commonly with replacement, and within each of these resamples, the estimate of interest is re-obtained. A large number of these estimate replicates can then be used to construct the empirical sampling distribution from which confidence intervals, bias, and variance may be estimated. These methods are particularly advantageous for statistics or estimators for which no standard methods apply or are difficult to derive.

The jackknife is a popular resampling method, first introduced by Quenouille in 1949 as a method of bias estimation. In 1958, jackknifing was both named by Tukey and expanded to include variance estimation. A jackknife is a multipurpose tool, similar to a swiss army knife, that can get its user out of tricky situations. Efron later developed the arguably most popular resampling method, the bootstrap, in 1979 after being inspired by the jackknife.

In Efron’s (1982) book The jackknife, the bootstrap, and other resampling plans, he states,

Good simple ideas, of which the jackknife is a prime example, are our most precious intellectual commodity, so there is no need to apologize for the easy mathematical level.

Despite existing since the 1940’s, resampling methods were infeasible due to the computational power required to perform resampling and recalculate estimates many times. With today’s computing power, the uncomplicated yet powerful jackknife, and resampling methods more generally, should be a tool in every analyst’s toolbox.

Leave-one-out jackknife algorithm

The use of different resampling schemes results in different resampling methods. For example, bootstrap methods commonly sample observations with replacement from the original sample of size , repeating this a large number of times to obtain a large number of replicates.

The leave-one-out (LOO) jackknife creates samples of size from the original sample of size by deleting each observation in turn. The leave-one-out jackknife is similar to the concept of leave-one-out crossvalidation encountered in prediction modelling or machine learning. More than one observation may be deleted at a time, though less common, in which case the method may be referred to as the leave-K-out jackknife.

The leave-one-out jackknife algorithm proceeds generally as follows:

1. Estimate the parameter or estimand of interest 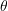using the original sample of size , referring to the resulting estimate as the full-sample estimate and denoting it by .
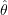2. Construct jackknife samples of size by deleting each observation in turn. That is,

   (1)  

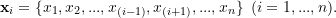
3. Estimate the parameter or estimand of interest within each jackknife sample, yielding jackknife replicates,

   (2)  

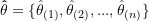
   where subscript 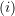is used to indicate exclusion of the 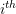sample observation.

4. Obtain the jackknife estimate 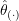as the mean of the jackknife replicates,

   (3)  

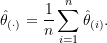
Bias estimation and adjustment

As noted, the jackknife was introduced by Quenouille in 1949 as a method of estimating bias.

Suppose is the full-sample estimate based on the entire sample of size and is our jackknife estimate obtained according to the algorithm in the previous section. The jackknife estimate of the bias, also known as Quenouille’s estimate, is then obtained as

(4)  

A bias-corrected jackknife estimate is then obtained as,

(5)  

If the full-sample estimate is unbiased such that , it follows that and the bias-corrected jackknife estimate is equivalent to the full-sample estimate and jackknifing provides no advantages with respect to bias.

If the full-sample estimate is biased such that , the bias-corrected jackknife estimate will always reduce the bias compared to the full-sample estimate! However, the bias will not always be reduced to zero depending on its structure.

Suppose we assume that for a sample of size , , the full-sample estimate is biased such that its expectation takes the form,

(6)  

where the do not depend on the sample size . Then, since each jackknife replicate is constructed using a jackknife sample of size , it follows that the expectation of the jackknife estimate is given by,

(7)  

That is, the expectation of the jackknife estimate is equivalent to the expectation of estimator of interest based on a sample of size . The expected difference between the full-sample estimate and the jackknife estimate is then,

(8)  

If the assumed bias structure is correct, approximates the first bias term of . However, if the bias structure features higher order bias terms, extensions of the jackknife, such as Quenouille’s second-order jackknife, may be required.

Pseudo-observations and variance estimation

Tukey (1958) noticed that the bias-corrected jackknife estimate could be expressed as the mean of pseudo-observations, defined for the sample observation as,

(9)  

such that,

(10)  

The pseudo-observation can be viewed or interpretted as the individual’s contribution to the estimate.

Tukey further conjectured that pseudo-observations could be treated as independent and identically distributed random variables. When true, estimating the variance of the bias-corrected jackknife estimate is equivalent to estimating the variance of mean of the pseudo-observations. That is,

(11)  

If is assumed to be asymptotically Normally distributed, confidence intervals for can be constructed in the usual manner as,

(12)  

Tukey’s conjectures were published in a short abstract with no supporting proofs. Miller (1968, 1974) later demonstrated that the properties conjectured only held for particular classes of statistics. However, this class of statistics does appear to include expectation functionals or linear functionals (among others)!

For more detail on expectation functionals and their estimators, check out my blog post U-, V-, and Dupree statistics.

• Tukey, J. W. (1958). Bias and confidence in not-quite large samples (Abstract). The Annals of Mathematical Statistics, 29(2), 614. doi:10.1214/aoms/1177706647
• Miller, R. G. (1968). Jackknifing Variances. The Annals of Mathematical Statistics, 39(2), 567–582. doi:10.1214/aoms/1177698418
• Miller, R. G. (1974). The Jackknife–A Review. Biometrika, 61(1), 1-15. doi:10.2307/2334280]

Example: Biased variance estimator

Data generation and estimator properties

In the following section, we demonstrate properties of the discussed jackknife estimators and pseudo-observations for the biased estimator of the variance with denominator ,

(13)  

The expectation of takes the form of described within the Bias section,

(14)  

with , and it follows that,

(15)  

When the are independent and identically distributed according to ,

(16)  

Here, we generate a sample of independent and identically distributed observations generated according to .

set.seed(12345)

n <- 100
mu <- 100
sigma <- 7

x <- rnorm(n, mu, sigma)

For reference, the first five generated observations are: 104.1, 105, 99.2, 96.8, 104.2.

A histogram of all generated observations is provided below.

qplot(x, geom='histogram', bins=5) + theme_bw()

It follows that the true properties of in this scenario are as follows.

trueBias <- -sigma^2/n
trueBias

## [1] -0.49

trueVar  <- 2 * (n-1) * sigma^4 / n^2
trueVar

## [1] 47.5398

That is, = -0.49 and = 47.54.

Leave-one-out jackknife algorithm

First, we obtain the full-sample estimate by applying a given Estimator to the sample x.

getFullEst <- function(x, Estimator){
  Estimator(x)
}

In this example, we are using the biased variance estimator so that Estimator = bVar.

bVar <- function(x){
  n <- length(x)
  bVar<- 1/n * sum((x-mean(x))^2)
  return(bVar)
}

FullEst <- getFullEst(x, bVar)

Thus, the full-sample estimate is 60.28.

Second, we use a loop to construct a list of the jackknife Samples of size by deleting each observation in turn.

getSamples <- function(x){
  n <- length(x)
  Samples <- list()
  for(i in 1:n){
    Samples[[i]] <- x[-i]
  }
  return(Samples)
}

Samples <- getSamples(x)

Inspecting the first five observations of the first sample, we can see that 104.1 has been deleted: 105, 99.2, 96.8, 104.2, 87.3, 104.4.

Third, we use sapply to apply Estimator to each of the Samples and store the resulting in a vector Replicates.

getReplicates <- function(Samples, Estimator){
  Replicates <- sapply(Samples, FUN=Estimator, simplify=T)
  return(Replicates)
}

Replicates <- getReplicates(Samples, bVar)

The first ten replicates, , are: 60.83, 60.78, 60.83, 60.64, 60.82, 58.76, 60.81, 60.75, 60.75, 60.21.

Fourth, we take the average of all jackknife Replicates to obtain the jackknife estimate JackEst.

getJackEst <- function(Replicates){
  n <- length(Replicates)
  JackEst <- mean(Replicates)
  return(list(JackEst=JackEst, n=n))
}

JackEst <- getJackEst(Replicates)

The resulting value of = 60.27.

Bias estimation and adjustment

To obtain a bias-corrected jackknife estimate, , we first need to obtain an estimate of the bias.

getBias <- function(FullEst, JackEst){
  n <- JackEst$n
  JackEst <- JackEst$JackEst
  Bias <- (n-1) * (JackEst - FullEst)
  return(Bias)
}

Bias <- getBias(FullEst, JackEst)

The estimated bias of the full-sample estimate is -0.609. Recall that the true bias is -0.49.

getAdjEst <- function(FullEst, Bias){
  AdjEst <- FullEst - Bias
  return(AdjEst)
}

AdjEst <- getAdjEst(FullEst, Bias)

Subtracting the estimated bias from the full-sample estimate yields a bias-adjusted jackknife estimate 60.89. Recall that the true value of and the full-sample estimate 60.28.

Pseudo-observations and variance estimation

To estimate the variance of our bias-adjusted jackknife estimate , we first need to transform each observation into a pseudo-observation .

getPseudoObs <- function(FullEst, Replicates){
  n <- length(Replicates)
  PseudoObs <- n*FullEst - (n-1)*Replicates
  return(PseudoObs)
}

PseudoObs <- getPseudoObs(FullEst, Replicates)

The first five pseudoobservations are: 5.73, 10.67, 6.22, 24.16, 6.44.

Finally, we obtain an estimate of the variance of as the sample variance of the sample mean of the pseudo-observations.

getVarAdj <- function(PseudoObs){
  n <- length(PseudoObs)
  Var <- (1/n) * var(PseudoObs)
  return(Var)
}

VarAdj <- getVarAdj(PseudoObs) 

The estimated variance of the bias-adjusted jackknife estimate is 53.89. Recall that the true value 47.54.

Summary

Based on our single sample of i.i.d observations from , the jackknife appears to have provided a reasonable estimate of the parameter of interest (est. = 60.89), the bias of the estimator = -0.49 (est. -0.61), and the variance of the estimator = 47.54 (est. = 53.89).

Discrepancies between true and estimated values are likely due to sampling variation (and the use of a single sample to evaluate the methods). If we repeat this process for 1,000 samples of size from and average the results across the samples, we would expect close approximation of the true values.

results <- data.frame(Bias=NA, AdjEst=NA, VarAdj=NA)

n_sim <- 1000
for(s in 1:n_sim){
  x <- rnorm(n, mu, sigma)
  
  FullEst <- getFullEst(x, bVar)
  Samples <- getSamples(x)
  Replicates <- getReplicates(Samples, bVar)
  JackEst <- getJackEst(Replicates)
  Bias <- getBias(FullEst, JackEst)
  AdjEst <- getAdjEst(FullEst, Bias)
  PseudoObs <- getPseudoObs(FullEst, Replicates)
  VarAdj <- getVarAdj(PseudoObs) 
  
  results[s,] <- c(Bias, AdjEst, VarAdj)
}

round(colMeans(results), 2)

##   Bias AdjEst VarAdj 
##  -0.49  49.01  48.32

Indeed, we recover the true value of the estimator, its bias, and variance almost exactly!