Overview
I’m currently working on a project that revolves around the EM algorithm, and am finally realizing the power of this machinery. It really is like that movie with Jim Carrey where he can’t stop seeing the number 23 everywhere, except for me it’s the EM algorithm. Apparently this is called THE BAADER-MEINHOF PHENOMENON, oooh that’s fancy. You’ve probably seen the EM algorithm around too – though perhaps you didn’t know it. It’s commonly used for estimation with missing data. A modified EM algorithm (EMis) is used by the Amelia library in R. The EM algorithm also underpins latent variable models, which makes sense because latent variables are really missing observations when you think about it, right?! The more I learn about statistics, the more I realize most things are really missing data problems… cough potential outcomes cough
Anyways, I was previously taught the EM algorithm using the classic multinomial example. This is a great teaching tool, but I’ve never run into a situation like this in my life (yet). But, I do run into mixture distributions a surprising amount – mostly when investigating heterogeneity within patient populations. There’s a whole textbook on this, see: Medical Applications of Finite Mixture Models. The EM algorithm makes a lot more sense to me in the context of mixture models:
- We sample a group of patients and observe their response.
- We notice a bimodal structure in the response distribution.
- We hypothesize the observed distribution actually corresponds to two subpopulations or “classes.”
- We don’t know who belongs to which subpopulation.
- We estimate the probability of latent class membership using the EM algorithm.
Wouldn’t ya know it, this is unsupervised clustering.
In this blog post, I motivate the EM algorithm in the context of a two-component Gaussian mixture model. A thorough walkthrough of the underlying theory is provided. In this case, estimators take a nice closed form, but this is rarely the case for complex problems encountered in practice. R code for implementating the EM algorithm using the closed form estimators is provided. I also demonstrate how this model can be easily fit using the flexmix library.
Figure: A two-component Gaussian mixture density.
Theory walkthrough
Density of a two-component Gaussian mixture
Consider a random sample of ![]() individuals. Let
individuals. Let ![]() represent their independent and identically distributed responses, which we assume arise from a two-component Gaussian mixture model. Individuals belong to the first component (i.e., subpopulation) with probability
represent their independent and identically distributed responses, which we assume arise from a two-component Gaussian mixture model. Individuals belong to the first component (i.e., subpopulation) with probability ![]() and to the second component with probability
and to the second component with probability ![]() . The (mixture) density of the responses is formally provided by,
. The (mixture) density of the responses is formally provided by,
![]()
where ![]() corresponds to the Normal density of the
corresponds to the Normal density of the ![]() subpopulation,
subpopulation, ![]() , with mean
, with mean ![]() and variance
and variance ![]() . Equivalently, in the simple two-class scenario, we can express this as:
. Equivalently, in the simple two-class scenario, we can express this as:
![]()
since ![]() . Thus, the mixture density is essentially an average of the two component densities, weighted by their respective component probabilities.
. Thus, the mixture density is essentially an average of the two component densities, weighted by their respective component probabilities.
Let ![]() represent the vector of all parameters. The corresponding likelihood is:
represent the vector of all parameters. The corresponding likelihood is:
![]()
and subsequently, the log-likelihood is:
![]()
While the density and corresponding (log) likelihoods appear simple in form, the weighted sum within the logarithm makes the log-likelihood ![]() surprisingly challenging to maximize. Maximum likelihood estimation with respect to mixture distributions is also notoriously ill-behaved (e.g., boundary problems, singularity). The EM algorithm reconceptualizes this problem to make our lives easier.
surprisingly challenging to maximize. Maximum likelihood estimation with respect to mixture distributions is also notoriously ill-behaved (e.g., boundary problems, singularity). The EM algorithm reconceptualizes this problem to make our lives easier.
Latent class membership
Now, suppose that for each individual there exists an unobserved or “latent” binary random variable ![]() which dictates their component membership.
which dictates their component membership.
Then, the (observed) ![]() can be re-expressed in terms of the (latent)
can be re-expressed in terms of the (latent) ![]() :
:
![]()
where the ![]() are random deviates distributed according to the
are random deviates distributed according to the ![]() density. That is,
density. That is, ![]() and
and ![]() . The
. The ![]() ,
, ![]() , and
, and ![]() are assumed to be independent.
are assumed to be independent.
Notice that by definition, the conditional density of ![]() given
given ![]() is simply the Normal density corresponding to the component indicated by
is simply the Normal density corresponding to the component indicated by ![]() . This can be compactly represented as:
. This can be compactly represented as:
![]()
That is, ![]() and
and ![]() .
.
Bayes’ Theorem tells us that ![]() . Plugging in
. Plugging in ![]() , and
, and ![]() , we obtain the joint density of
, we obtain the joint density of ![]() and
and ![]() :
:
![]()
We can see that the density of the ![]() remains
remains ![]() as defined above by simply marginalizing (i.e., summing) the joint distribution over the distinct values of
as defined above by simply marginalizing (i.e., summing) the joint distribution over the distinct values of ![]() :
:
![]()
Complete data likelihood
Although we obtain the same density for ![]() as before, the advantage redefining the
as before, the advantage redefining the ![]() in this way is that we can now work with the joint distribution
in this way is that we can now work with the joint distribution ![]() .
. ![]() is much better suited to logarithmic transformation due to its product representation, unlike the marginal distribution
is much better suited to logarithmic transformation due to its product representation, unlike the marginal distribution ![]() . This allows us to simplify estimation significantly.
. This allows us to simplify estimation significantly.
If we observed both ![]() and
and ![]() , the complete data likelihood would take the form:
, the complete data likelihood would take the form:
![]()
and subsequently, the complete data log-likelihood is:
![]()
Notice two things: (1) the logarithm now acts directly on the Normal densities; and (2) the complete data log-likelihood is simply the sum of contributions from the two components. As a result, derivatives of the complete data log-likelihood will be extremely straightforward to calculate.
Conditional expectation of complete log-likelihood
Of course, we can’t actually observe ![]() , so we cannot maximize the complete data log-likelihood directly. But, recall that conditional expectations are only functions of the parameters and the conditioning random variable. Thus, by taking the expectation of the complete data log-likelihood conditional on the observed
, so we cannot maximize the complete data log-likelihood directly. But, recall that conditional expectations are only functions of the parameters and the conditioning random variable. Thus, by taking the expectation of the complete data log-likelihood conditional on the observed ![]() , we get something we can actually maximize directly. When we condition on
, we get something we can actually maximize directly. When we condition on ![]() , the terms within the squiggly brackets of
, the terms within the squiggly brackets of ![]() can be treated as fixed, implying that:
can be treated as fixed, implying that:
![]()
Using our previous work, we can easily derive the density of ![]() conditional on
conditional on ![]() :
:
![]()
Now, note that ![]() and similarly
and similarly ![]() .
.
Plugging ![]() into the conditional expectation, we obtain:
into the conditional expectation, we obtain:
![]()
where:
![]()
![]()
The conditional expectation of the complete log-likelihood no longer features the unobserved ![]() which is nice. But, it does feature
which is nice. But, it does feature ![]() – so how can we estimate these parameters?
– so how can we estimate these parameters?
The EM algorithm
We can maximize the expected complete log-likelihood with respect to ![]() , treating the weights
, treating the weights ![]() as fixed. To do so, we need to use iteration. In essence:
as fixed. To do so, we need to use iteration. In essence:
- Estimation: Initial parameter values
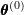 are used to estimate the weights
are used to estimate the weights 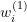 .
. - Maximization: The conditional expectation of the complete log-likelihood is then maximized with respect to
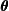 , treating the
, treating the 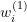 as constant, and yielding
as constant, and yielding 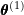 .
.
The expectation and maximization steps are then repeated until convergence is reached. Hence, the “EM” algorithm!
Formally, at the ![]() iteration, we consider the objective function:
iteration, we consider the objective function:
![]()
where
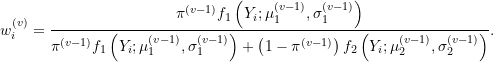
Notice that weights at the ![]() step are estimated using parameter estimates from the previous
step are estimated using parameter estimates from the previous ![]() step. The EM algorithm then proceeds as follows:
step. The EM algorithm then proceeds as follows:
- Initialize the parameter vector,
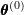 .
. - E-step: Estimate the weights
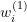 using
using 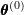 .
. - M-step: Maximize the objective function with respect to
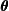 to obtain
to obtain 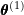 :
:
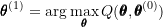
- Check for convergence in
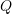 or the parameter vector. If convergence is met, stop. Else, repeat steps 2 through 4.
or the parameter vector. If convergence is met, stop. Else, repeat steps 2 through 4.
Note: The performance of the EM algorithm is very sensitive to initialization. A commonly used strategy is to apply the ![]() -means clustering algorithm, and then estimate parameters within each cluster (demonstrated shortly).
-means clustering algorithm, and then estimate parameters within each cluster (demonstrated shortly).
Analytic form of the M-step
For this simple problem, the M-step can be represented as a set of formulas for each entry in the parameter vector ![]() . Recall that the
. Recall that the ![]() Normal density is provided by,
Normal density is provided by,
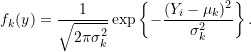
Plugging this into our objective function (and ignoring the constant ![]() ), we obtain:
), we obtain:
![]()
![]()
To simplify notation, let ![]() . Taking partial derivatives with respect to each parameter provides:
. Taking partial derivatives with respect to each parameter provides:
![]()
![]()
![]()
Let ![]() , which can be interpreted as “the effective number of subjects assigned to mixture component 1” at iteration
, which can be interpreted as “the effective number of subjects assigned to mixture component 1” at iteration ![]() . Setting each partial derivative equal to zero and solving provides estimators:
. Setting each partial derivative equal to zero and solving provides estimators:
![]()
![]()
![]()
Similar results are obtained for ![]() and
and ![]() , with
, with ![]() replaced by
replaced by ![]() and
and ![]() replaced by
replaced by ![]() . Thus, estimators at the
. Thus, estimators at the ![]() iteration are weighted estimators, where the weights represent the estimated class membership proportions from the
iteration are weighted estimators, where the weights represent the estimated class membership proportions from the ![]() iteration.
iteration.
Implementation
Data generation
We set the following:
- Sample size to
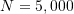 ;
; 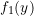 equal to
equal to 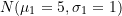 ;
;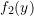 equal to
equal to 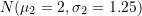 ;
;- Mixing probability equal to
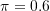 .
.
The following chunk generates data from the specified mixture by first sampling the true value of the latent class ![]() from a Bernoulli distribution. Based on the drawn
from a Bernoulli distribution. Based on the drawn ![]() , the response
, the response ![]() is generated from the corresponding Normal density.
is generated from the corresponding Normal density.
library(tidyverse)
set.seed(12345)
# Simulate two-component Gaussian mixture
## Sample size
N = 5000
## Parameters for first component
mu1 <- 5; sigma1 <- 1
## Parameters for second component
mu2 <- 2; sigma2 <- 1.25
## Mixing probability
pi <- 0.6
## True parameter vector
truth <- c(pi, mu1, sigma1, mu2, sigma2)
## Sample latent class
z <- rbinom(n=N, size=1, prob=pi)
## Sample response based on latent class
y1 <- rnorm(n=sum(z==1), mean=mu1, sd=sigma1)
y2 <- rnorm(n=sum(z==0), mean=mu2, sd=sigma2)
# Combine all responses into a single vector
y <- c(y1, y2)
## Visualize mixture distribution
qplot(x=y, geom=c('histogram')) +
labs(x='Observed response, y', y='Observed frequency') +
theme_bw()
Figure: Histogram of N=5000 responses generated from our two-component Gaussian mixture.
From scratch: analytic estimators
Helper functions
It is helpful to first define all functions we will need for our EM algorithm. In the following chunks, we define 5 functions:
- f1: The density of the first component
- f2: The density of the second component
- estep: The estimation step, which calculates the weights
- mstep: The maximization step, which updates parameter estimates
- ll: The objective function, which calculates the value of the weighted log-likelihood based on current parameter estimates.
The density functions are simply reskinned versions of dnorm, to align with the notation used here.
# First density
f1 <- function(y, mu1, sigma1){
dnorm(y, mean=mu1, sd=sigma1)
}
# Second density
f2 <- function(y, mu2, sigma2){
dnorm(y, mean=mu2, sd=sigma2)
}
The E-step uses parameter estimates from the previous step to update weights at the current step.
# E-step: update weights
estep <- function(y, pi1, mu1, sigma1, mu2, sigma2){
pi2 <- 1 - pi1
w1_num <- pi1 * f1(y, mu1, sigma1)
w1_den <- pi1 * f1(y, mu1, sigma1) + pi2 * f2(y, mu2, sigma2)
w1 <- w1_num / w1_den
return(w1)
}
The M-step uses the updated weights to update parameter estimates. Notice we are estimating ![]() here rather than
here rather than ![]() , hence the square root.
, hence the square root.
# M-step: update parameter estimates
mstep <- function(y, w1){
# weights of component 2
w2 <- 1 - w1
# mixture probability
pi1 <- sum(w1)/N
# first component params
mu1 <- sum(w1 * y) / sum(w1)
sigma1 <- sqrt(sum(w1 * (y-mu1)^2) / sum(w1))
# second component params
mu2 <- sum(w2 * y) / sum(w2)
sigma2 <- sqrt(sum(w2 * (y-mu2)^2) / sum(w2))
# estimated parameter vector
est <- c(pi1, mu1, sigma1, mu2, sigma2)
return(est)
}
Finally, we calculate the value of the weighted log-likelihood (objective function) based on the current parameter estimates in order to check convergence.
# Log-likelihood: calculate weighted log-likelihood based on parameter est
ll <- function(y, pi1, mu1, sigma1, mu2, sigma2){
pi2 <- 1 - pi1
inner <- log(pi1 * f1(y, mu1, sigma1) + pi2 * f2(y, mu2, sigma2))
ll <- sum(inner)
return(ll)
}
Putting it all together
We allow for a maximum of ![]() iterations of the EM algorithm. If the value of the objective function at the current step is less than some tolerance greater than that at the previous step, iteration is stopped.
iterations of the EM algorithm. If the value of the objective function at the current step is less than some tolerance greater than that at the previous step, iteration is stopped.
Parameter estimates at each iteration are stored within the vector est_list while the value of the objective function is stored within the vector ll_vec. This will allow us to see how our EM algorithm converges!
On the first iteration, b=1, the k-means algorithm is applied the observed responses with ![]() . Estimates of the parameters are then obtained within the two predicted clusters to serve as inital values.
. Estimates of the parameters are then obtained within the two predicted clusters to serve as inital values.
ll_vec <- c()
est_list <- list()
for (b in 1:1000){
# Initialize parameter values
if (b==1){
# Apply k-means with two centers
kinit <- kmeans(y, centers=2)
# Store predicted cluster labels
cluster <- kinit$cluster
# Estimate mixture probability
pi1 <- sum(cluster==1)/N
# Estimate first component parameters
y1 <- y[cluster==1]
mu1 <- mean(y1)
sigma1 <- sd(y1)
# Estimate second component parameters
y2 <- y[cluster==2]
mu2 <- mean(y2)
sigma2 <- sd(y2)
# Objective function
obj <- ll(y, pi1, mu1, sigma1, mu2, sigma2)
}
else {
# Iterative updating
# estep
w1 <- estep(y, pi1, mu1, sigma1, mu2, sigma2)
# mstep
est <- mstep(y, w1)
pi1 <- est[1]
mu1 <- est[2] ; sigma1 <- est[3]
mu2 <- est[4] ; sigma2 <- est[5]
# value of objective function
obj <- ll(y, pi1, mu1, sigma1, mu2, sigma2)
}
# Update log-likelihood vector and estimate list
ll_vec[b] <- obj
est_list[[b]] <- c('pi1'=pi1,
'mu1'=mu1, 'sigma1'=sigma1,
'mu2'=mu2, 'sigma2'=sigma2)
if (b > 2) { if (ll_vec[b] - ll_vec[(b-1)] < 0.001) break }
}
We get pretty dang close to the truth with only 61 iterations using the EM algorithm!
rbind(c('True values', truth),
c('Inital estimate', round(est_list[[1]], 3)),
c('Best estimate', round(est_list[[length(ll_vec)]], 3)))
## pi1 mu1 sigma1 mu2 sigma2 ## [1,] "True values" "0.6" "5" "1" "2" "1.25" ## [2,] "Inital estimate" "0.375" "1.756" "1.052" "5.002" "0.917" ## [3,] "Best estimate" "0.404" "1.994" "1.277" "5.001" "0.981"
rbind(c('Best log-lik', round(ll_vec[length(ll_vec)], 3)),
c('No. of iter', length(ll_vec)))
## [,1] [,2] ## [1,] "Best log-lik" "-9844.273" ## [2,] "No. of iter" "61"
plot(ll_vec, type='l')
You might notice that the component labels produced by our algorithm are opposite what we defined, i.e., class 1 and 2 are switched so ![]() rather than
rather than ![]() . That’s because labels are not unique! But that’s okay, we are smart enough to recognize which class is which here… This can get a bit dicey in more complex scenarios, however.
. That’s because labels are not unique! But that’s okay, we are smart enough to recognize which class is which here… This can get a bit dicey in more complex scenarios, however.
Out-of-the-box: using flexmix
flexmix is a fantastic package which revolves fitting mixture distributions and provides, you guessed it, a lot of flexibility.
library(flexmix)
To use flexmix for this simple scenario, we create a dataframe with our observed responses.
df <- data.frame(y=y)
Then, we apply the flexmix function, first specifying the model for the responses. Here, we simply use ~1 to specify no covariates. Then, we specify the number of components k=2 and the distribution of the responses (here Gaussian).
m1 <- flexmix(y ~ 1, data=df, k=2, model = FLXMRglm(family='gaussian'))
m1
## ## Call: ## flexmix(formula = y ~ 1, data = df, k = 2, model = FLXMRglm(family = "gaussian")) ## ## Cluster sizes: ## 1 2 ## 1949 3051 ## ## convergence after 101 iterations
cbind(parameters(m1, component=1), parameters(m1, component=2))
## Comp.1 Comp.2 ## coef.(Intercept) 2.044882 5.0225334 ## sigma 1.303764 0.9701286
We see very similar results from both implementations! With 101 iterations, the mixing probability is estimated by flexmix as 1949/3051 = 0.64, so the estimated parameters are (0.64, 5.02, 0.97, 2.04, 1.30). Lovely.
And they all lived happily ever after
Hope you found this helpful! In the future, I hope to discuss more complicated extensions such as mixtures of linear regressions which allows responses to depend on covariates, and mixture of experts models which allow both responses and class probabilities to depend on covariates! In these cases, I will also explore how optim can be used to maximize the objective function when closed form estimators are not available.

2 thoughts on “Embracing the EM algorithm: One continuous response”