Thank you very much to the lovely Feben Alemu for pointing me in the direction of https://pungenerator.org/ as a means of ensuring we never have to go without a brilliant title! With great power comes great responsibility.

Review
Statistical functionals are any real-valued function of a distribution function ![]() ,
, ![]() . When
. When ![]() is unknown, nonparametric estimation only requires that
is unknown, nonparametric estimation only requires that ![]() belong to a broad class of distribution functions
belong to a broad class of distribution functions ![]() , typically subject only to mild restrictions such as continuity or existence of specific moments.
, typically subject only to mild restrictions such as continuity or existence of specific moments.
For a single independent and identically distributed random sample of size ![]() ,
, ![]() , a statistical functional
, a statistical functional ![]() is said to belong to the family of expectation functionals if:
is said to belong to the family of expectation functionals if:
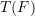 takes the form of an expectation of a function
takes the form of an expectation of a function 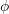 with respect to
with respect to 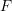 ,
,
![Rendered by QuickLaTeX.com \[T(F) = \mathbb{E}_F~ \phi(X_1, …, X_a) \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-4b10dae4aa2f3621fc36c4e99fec5e69_l3.png)
 is a symmetric kernel of degree
is a symmetric kernel of degree 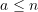 .
.
A kernel is symmetric if its arguments can be permuted without changing its value. For example, if the degree ![]() ,
, ![]() is symmetric if
is symmetric if ![]() .
.
If ![]() is an expecation functional and the class of distribution functions
is an expecation functional and the class of distribution functions ![]() is broad enough, an unbiased estimator of
is broad enough, an unbiased estimator of ![]() can always be constructed. This estimator is known as a U-statistic and takes the form,
can always be constructed. This estimator is known as a U-statistic and takes the form,
![]()
such that ![]() is the average of
is the average of ![]() evaluated at all
evaluated at all ![]() distinct combinations of size
distinct combinations of size ![]() from
from ![]() .
.
For more detail on expectation functionals and their estimators, check out my blog post U-, V-, and Dupree statistics.
Since each ![]() appears in more than one summand of
appears in more than one summand of ![]() , the central limit theorem cannot be used to derive the limiting distribution of
, the central limit theorem cannot be used to derive the limiting distribution of ![]() as it is the sum of dependent terms. However, clever conditioning arguments can be used to show that
as it is the sum of dependent terms. However, clever conditioning arguments can be used to show that ![]() is in fact asymptotically normal with mean
is in fact asymptotically normal with mean
![]()
and variance
![]()
where
![]()
The sketch of the proof is as follows:
- Express the variance of
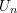 in terms of the covariance of its summands,
in terms of the covariance of its summands,
![Rendered by QuickLaTeX.com \[\text{Var}_{F}~ U_n = \frac{1}{{n \choose a}^2} \mathop{\sum \sum} \limits_{\substack{1 \leq i_1 < ... < i_{a} \leq n \\ 1 \leq j_1 < ... < j_{a} \leq n}} \text{Cov}\left[\phi(X_{i_1}, ..., X_{i_a}),~ \phi(X_{j_1}, ..., X_{j_a})\right].\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-a2c21d5d7f01714fd65d97bc9e5366a0_l3.png)
- Recognize that if two terms share
 common elements such that,
common elements such that,
![Rendered by QuickLaTeX.com \[ \text{Cov} [\phi(X_1, …, X_c, X_{c+1}, …, X_a), \phi(X_1, …, X_c, X'_{c+1}, …, X'_a)] \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-0afd7ad44b3d54edda4f587055601b06_l3.png)
conditioning on their
 shared elements will make the two terms independent.
shared elements will make the two terms independent. - For
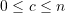 , define
, define
![Rendered by QuickLaTeX.com \[\phi_c(X_1, …, X_c) = \mathbb{E}_F \Big[\phi(X_1, …, X_a) | X_1, …, X_c \Big] \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-e5321ca7cbb2cc4e8035f405360737f8_l3.png)
such that
![Rendered by QuickLaTeX.com \[\mathbb{E}_F~ \phi_c(X_1, …, X_c) = \theta = T(F)\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-59b21c2f5cd533c3e54b99fef2e75a88_l3.png)
and
![Rendered by QuickLaTeX.com \[\sigma_{c}^2 = \text{Var}_{F}~ \phi_c(X_1, …, X_c).\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-5eae440995d70a60fcada6fcb85ecc89_l3.png)
Note that when
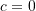 ,
, 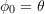 and
and 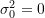 , and when
, and when  ,
, 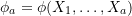 and
and 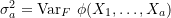 .
. - Use the law of iterated expecation to demonstrate that
![Rendered by QuickLaTeX.com \[ \sigma^{2}_c = \text{Cov} [\phi(X_1, …, X_c, X_{c+1}, …, X_a), \phi(X_1, …, X_c, X'_{c+1}, …, X'_a)] \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-ae2bc59e8a4485598141edc5f81b9a3d_l3.png)
and re-express
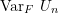 as the sum of the
as the sum of the 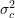 ,
,![Rendered by QuickLaTeX.com \[ \text{Var}_F~U_n = \frac{1}{{n \choose a}} \sum_{c=1}^{a} {a \choose c}{n-a \choose a-c} \sigma^{2}_c.\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-eeb9812359c7a08762e2d186b4ffecfd_l3.png)
Recognizing that the first variance term dominates for large
 , approximate
, approximate 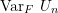 as
as![Rendered by QuickLaTeX.com \[\text{Var}_F~U_n \sim \frac{a^2}{n} \sigma^{2}_1.\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-2561ada44c52b7270d503a3b65cc4bdb_l3.png)
- Identify a surrogate
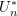 that has the same mean and variance as
that has the same mean and variance as 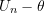 but is the sum of independent terms,
but is the sum of independent terms,
![Rendered by QuickLaTeX.com \[ U_n^{*} = \sum_{i=1}^{n} \mathbb{E}_F [U_n - \theta|X_i] \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-6279990329ef07296dfeb6bf7e3ff6ea_l3.png)
so that the central limit may be used to show
![Rendered by QuickLaTeX.com \[ \sqrt{n} U_n^{*} \rightarrow N(0, a^2 \sigma_1^2).\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-a5374b23424474a55f28fc80a9eca29d_l3.png)
- Demonstrate that
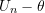 and
and 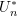 converge in probability,
converge in probability,
![Rendered by QuickLaTeX.com \[ \sqrt{n} \Big((U_n - \theta) - U_n^{*}\Big) \stackrel{P}{\rightarrow} 0 \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-03f17552990655c5c7bc7b2446eb452f_l3.png)
and thus have the same limiting distribution so that
![Rendered by QuickLaTeX.com \[\sqrt{n} (U_n - \theta) \rightarrow N(0, a^2 \sigma_1^2).\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-9e47c6463a7f5a734945b178bfc8dfad_l3.png)
For a walkthrough derivation of the limiting distribution of ![]() for a single sample, check out my blog post Getting to know U: the asymptotic distribution of a single U-statistic.
for a single sample, check out my blog post Getting to know U: the asymptotic distribution of a single U-statistic.
This blog post aims to provide an overview of the extension of kernels, expectation functionals, and the definition and distribution of U-statistics to multiple independent samples, with particular focus on the common two-sample scenario.
Definitions for multiple independent samples
Consider ![]() independent random samples denoted
independent random samples denoted
![]()
where ![]() is the size of the
is the size of the ![]() sample and
sample and ![]() is the total sample size. Let
is the total sample size. Let ![]() . Then, for multiple independent samples, a statistical functional
. Then, for multiple independent samples, a statistical functional ![]() is an expectation functional if
is an expectation functional if
![]()
where the kernel ![]() is a function symmetric within each of the
is a function symmetric within each of the ![]() blocks of arguments
blocks of arguments ![]() , …,
, …, ![]() . That is, each block of arguments within
. That is, each block of arguments within ![]() can be permuted independently without changing the value of
can be permuted independently without changing the value of ![]() . By this definition,
. By this definition, ![]() is an unbiased estimator of
is an unbiased estimator of ![]() .
.
In the single sample case, we were able to permute all ![]() arguments of
arguments of ![]() without impacting
without impacting ![]() ‘s value as each
‘s value as each ![]() was identically distributed and thus “exchangeable”. Here, all
was identically distributed and thus “exchangeable”. Here, all ![]() arguments are not identically distributed.
arguments are not identically distributed.
The first sample may be distributed according to ![]() , the second according to
, the second according to ![]() , and so on. We have not required that
, and so on. We have not required that ![]() and so we cannot assume all
and so we cannot assume all ![]() arguments are exchangeable in the multiple sample scenario. Instead, we are restricted to permuting arguments within each sample.
arguments are exchangeable in the multiple sample scenario. Instead, we are restricted to permuting arguments within each sample.
Since we have assumed that the ![]() samples are independent, permuting one sample’s, or block’s, arguments should not impact the other blocks. Hence, our new block-based definition of a symmetric kernel.
samples are independent, permuting one sample’s, or block’s, arguments should not impact the other blocks. Hence, our new block-based definition of a symmetric kernel.
Since ![]() is symmetric within each block of arguments, we can require
is symmetric within each block of arguments, we can require
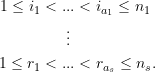
Then, from each of the ![]() independent samples, we require
independent samples, we require ![]() of the possible
of the possible ![]() arguments, so that there are a total of
arguments, so that there are a total of
![]()
possible combinations of the ![]() arguments.
arguments.
The U-statistic for ![]() independent samples is then defined analogously to that of a single sample,
independent samples is then defined analogously to that of a single sample,
![Rendered by QuickLaTeX.com \[U = \frac{1}{{n_1 \choose a_1} … {n_s \choose a_s}} \mathop{\sum … \sum} \limits_{\substack{1 \leq i_1 < ... < i_{a_1} \leq n_1 \\ \vdots \\ 1 \leq r_1 < ... < r_{a_s} \leq n_s}} \phi(X_{1{i_1}}, ..., X_{1i_{a_1}}; ... ; X_{s{r_1}}, ... X_{s{r_{a_s}}})\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-9afa3042584db960cb5a37eafd65ef72_l3.png)
so that ![]() is the average of
is the average of ![]() evaluated at all
evaluated at all ![]() independent combinations of the
independent combinations of the ![]() blocks’ arguments.
blocks’ arguments.
This notation got real ugly real fast but I promise that we will pretend that the two-sample case is the only important case soon enough.
Asymptotic distribution
As you can imagine, the derivation of the asymptotic distribution of ![]() for multiple samples is a notational nightmare. As a result, I will provide a sketch of the required elements. The remainder of the proof follows the logic of that of a single sample.
for multiple samples is a notational nightmare. As a result, I will provide a sketch of the required elements. The remainder of the proof follows the logic of that of a single sample.
The variance of ![]() can be expressed in terms of the covariance of its summands. We start, once again, by focusing on a single covariance term. To “simplify notation”, we consider
can be expressed in terms of the covariance of its summands. We start, once again, by focusing on a single covariance term. To “simplify notation”, we consider
![]()
Let ![]() represent the number of elements common to the
represent the number of elements common to the ![]() block of the two terms such that,
block of the two terms such that,
![]()
Conditioning on all ![]() common elements will make the two terms conditionally independent. Thus, we can define the multiple sample analogue to the single sample
common elements will make the two terms conditionally independent. Thus, we can define the multiple sample analogue to the single sample ![]() . For
. For ![]() ,
,
![Rendered by QuickLaTeX.com \begin{align*} \phi_{j_1, …, j_s} &(X_{11}, … X_{1j_1}; …; X_{s1}, …,;X_{sj_s}) \\ &= \mathbb{E}_F \Big[ \phi(X_{11}, …, X_{1a_1}; …; X_{s1}, …, X_{sa_s}) | X_{11}, … X_{1j_1}; …; X_{s1}, …, X_{sj_s}\Big] \end{align*}](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-38548003c4347f2e3453ffa2096e8d7c_l3.png)
and its variance as,
![Rendered by QuickLaTeX.com \begin{align*} \sigma^{2}_{j_1, …, j_s} = \text{Var}_F~ &\phi_{j_1, …, j_s} (X_{11}, … X_{1j_1}; …; X_{s1}, …, X_{sj_s}) \\ =\text{Cov}[&\phi(X_{11}, …, X_{1{j_1}}, X_{1{(j_1 + 1)}}, …, X_{1{a_1}};…;X_{s1}, …, X_{s{j_s}}, X_{s{(j_s + 1)}}, …, X_{s{j_s}}), \\ &\phi(X_{11}, …, X_{1{j_1}}, X'_{1{(j_1 + 1)}}, …, X'_{1{a_1}};…;X_{s1}, …, X_{s{j_s}}, X'_{s{(j_s + 1)}}, …, X'_{s{j_s}})]. \end{align*}](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-86c4dbf677c3df5645d230121ada50c2_l3.png)
Expressing ![]() in terms of
in terms of ![]() , it can be shown that
, it can be shown that
![]()
when all the variance components are finite and
![]()
Thus, the variance of ![]() is essentially the sum of the variance components obtained by conditioning on a single element within each of the
is essentially the sum of the variance components obtained by conditioning on a single element within each of the ![]() samples, or in each of the
samples, or in each of the ![]() blocks.
blocks.
Finally, it can be shown
![]()
Two-sample scenario
Consider two independent samples denoted ![]() and
and ![]() . The two-sample U-statistic for
. The two-sample U-statistic for ![]() and
and ![]() is,
is,
![Rendered by QuickLaTeX.com \[ U = \frac{1}{{m \choose a}{n \choose b}} \mathop{\sum \sum} \limits_{\substack{1 \leq i_1 < ... < i_{a} \leq m \\ 1 \leq j_1 < ... < j_b \leq n}} \phi(X_{i_1}, ..., X_{i_a}; Y_{j_1}, ..., Y_{j_b}). \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-01a00cdd4ce396510f035ae3dde6507c_l3.png)
If ![]() , conditioning on
, conditioning on ![]() elements of
elements of ![]() and
and ![]() elements of
elements of ![]() ,
,
![Rendered by QuickLaTeX.com \begin{align*} \phi_{ij}(X_1, …, X_i&; Y_1, …, Y_j) = \\ & \mathbb{E}_P \Big[\phi(X_1, …, X_a; Y_1, …, Y_b) | X_1, …, X_i; Y_1, …, Y_j \Big] \end{align*}](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-98792369c0bee68bcd54ebc76f47ddb7_l3.png)
and
![Rendered by QuickLaTeX.com \begin{align*} \sigma^{2}_{ij} = \text{Var}_{P}~& \phi_{ij} (X_1, …, X_i; Y_1, …, Y_j) \\ = \text{Cov} [&\phi(X_1, …, X_i, X_{i+1}, …, X_a; Y_1, …, Y_j, Y_{j+1}, …, Y_b), \\ &\phi(X_1, …, X_i, X'_{i+1}, …, X'_a; Y_1, …, Y_j, Y'_{j+1}, …, Y'_b)]. \end{align*}](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-6d6c0b858b3d9bb5ae179f4299035fb2_l3.png)
Then for ![]() and
and ![]() , we obtain
, we obtain
![]()
and similarly for ![]() and
and ![]() ,
,
![]()
If ![]() and
and ![]() are finite and
are finite and
![]()
then we can approximate the limiting variance of ![]() as
as
![]()
such that
![]()
At this point, you may be wondering what the heck are these variance components and how am I supposed to estimate them. In my next blog post, I promise that I will provide some examples of common one and two-sample U-statistics and their limiting distributions using our results!
For examples of common one- and two-sample U-statistics and their limiting distribution, check out One, Two, U: Examples of common one- and two-sample U-statistics.
Click here to download this blog post as an RMarkdown (.Rmd) file!

2 thoughts on “Much Two U About Nothing: Extension of U-statistics to multiple independent samples”