Plug-in estimators of statistical functionals

Consider a sequence of $n$ independent and identically distributed random variables $X_1, X_2, …, X_n \sim F$ . The distribution function $F$ is unknown but belongs to a known set of distribution functions $\mathcal{F}$ . In parametric estimation, $\mathcal{F}$ may represent a family of distributions specified by a vector of parameters, such as $(\mu, \sigma)$ in the case of the location-scale family. In nonparametric estimation, $\mathcal{F}$ is much more broad and is subject to milder restrictions, such as the existence of moments or continuity. For example, we may define $\mathcal{F}$ as the family of distributions for which the mean exists or all distributions defined on the real line $\mathbb{R}$ .

As mentioned in my previous blog post comparing nonparametric and parametric estimation, a statistical functional is any real-valued function of the cumulative distribution function $F$ , denoted $\theta = T(F)$ . Statistical functionals can be thought of as characteristics of $F$ , and include moments

$T(F) = \mathbb{E}_{F}[X^{k}]$

and quantiles

$T(F) = F^{-1}(p)$

as examples.

An infinite population may be considered as completely determined by its distribution function, and any numerical characteristic of an infinite population with distribution function $F$ that is used in statistics is a [statistical] functional of $F$ .

Wassily Hoeffding. “A Class of Statistics with Asymptotically Normal Distribution.” Ann. Math. Statist. 19 (3) 293 – 325, September, 1948.

This blog post aims to provide insight into estimators of statistical functionals based on a sample of $n$ independent and identically random variables, known as plug-in estimators or empirical functionals.

Expectation with respect to CDF

Many statistical functionals are expressed as the expectation of a real-valued function $g(x)$ with respect to $F$ . That is, for a single random variable $X$ ,

$\theta = T(F) = \mathbb{E}_{F} ~g(X).$

For example, the population mean can be expressed as

$\mu = \mathbb{E}_{F} ~X$

and the population variance can be expressed as

$\sigma^2 = \mathbb{E}_{F} ~(X - \mathbb{E}_{F} ~X)^2.$

What does it mean to take the expectation of a function $g$ of a random variable $X$ with respect to a distribution function $F$ ? Formally,

$\mathbb{E}_{F} ~g(X) = \int g(x) ~ dF(x)$

which takes the form of a Riemann-Stieltjes integral. We can re-express this integral so that it takes a more familiar form.

If 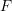$F$ is discrete, 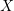$X$ has a corresponding mass function 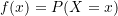$f(x) = P(X = x)$ such that
$\mathbb{E}_{F}~g(X) = \sum_{x} g(x)~ f(x) = \sum_{x} g(x)~ P(X = x).$
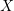If $F$ is continuous, $X$ has a corresponding density function 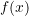$f(x)$ such that
$\mathbb{E}_{F}~g(X) = \int_{X} g(x) f(x) ~dx.$

This is just the usual form of the expectation of a function of a random variable per the Law of the unconcious statistician. The extension to two or more independent random variables is straight-forward,

$\mathbb{E}_{F_1, …, F_n} ~g(X_1, …, X_n) = \int …\int g(x_1, …, x_n) dF_1(x) …dF_n(x).$

Empirical cumulative distribution function

A natural estimator of $F$ is the empirical cumulative distribution function (ECDF), defined as

$\hat{F}_{n}(t) = \frac{1}{n} \sum_{i=1}^{n} \mathbb{I}(X_i \leq t)$

where $\mathbb{I}(\cdot)$ is an indicator function taking the value 1 if its argument is true and 0 otherwise. That is, the estimated probability that $X \leq t$ is the sample proportion of observations less than or equal to $t$ . Then, for a given value of $t$ , it is easy to show that $\hat{F}_{n}(t)$ is a consistent estimator of $F(t)$ .

Let $Z$ represent the number of $X$ ‘s less than or equal to $t$ . Then, $Z$ is distributed according to a Binomial distribution with $n$ trials and success probability $p = F(t)$ . That is, $Z \sim \text{Binomial}(n, F(t))$ . The sample estimate $\hat{p}$ of the success probability is then $\hat{F}_{n}(t)$ . The central limit theorem tells us that for a sample proportion $p$ ,

$\sqrt{n} (\hat{p} - p) \rightarrow N(0, ~p(1 - p))$

and thus, it follows that for fixed $t$ ,

$\sqrt{n} (\hat{F}_{n}(t) - F(t)) \rightarrow N(F(t), ~F(t) (1 - F(t))).$

Note that a stronger result is available for all $t$ simultaneously,

$\sup_{t} |\hat{F}_{n}(t) - F(t)| \stackrel{P}{\rightarrow} 0 ~\text{as}~ n \rightarrow 0.$

The ECDF can be implemented in R from scratch using the following code.

set.seed(12345)

library(tidyverse)

# Generate n = 100 observations from N(5, 1)
n = 100
X = rnorm(n, mean = 5, sd = 1)

# Specify range of x's for ECDF
X_min = min(X) - 1
X_max = max(X) + 1

# Create a sequence of t's to evaluate ECDF
t_eval = seq(X_min, X_max, 0.01)

# Estimate ECDF from scratch
Fn <- c()
for (t in t_eval){

  Ix <- ifelse(X <= t, 1, 0)    # I(Xi <= x)
  Fx <- (1/n) * sum(Ix)         # Defn of Fn(x)
  Fn <- append(Fn, Fx)          # Add result to Fn vector

}

# Plot ECDF 
qplot(x = t_eval, y = Fn, geom = 'step') +
  labs(x = 't', y = 'ECDF(t)', title = 'ECDF of random sample of size n = 100 from N(5, 1)') +
  lims(x = c(2, 8)) +
  theme_bw()

plot of chunk unnamed-chunk-1
Alternatively, the ECDF can be generated using R’s built-in ecdf function, which provides convenient methods such as plotting and quantiles.

Fn <- ecdf(X)
plot(Fn)

plot of chunk unnamed-chunk-2

quantile(Fn, 0.75)

##     75% 
## 5.90039

Empirical functionals, or plug-in estimators

Statistical functionals can be naturally estimated by an empirical functional which substitutes $\hat{F}_n$ for $F$ such that $\hat{\theta} = T(\hat{F}_n)$ . For this reason, empirical functionals are also commonly referred to as plug-in estimators.

$\hat{F}_{n}$ is a valid, discrete CDF which assigns mass $\frac{1}{n}$ to each of the observed $X_i, ~ i = 1, …, n$ . For a random variable $Y \sim \hat{F}_{n}$ ,

$P(Y \leq t) = \hat{F}_{n}(t) = \frac{1}{n} \sum_{i=1}^{n} \mathbb{I}(X_i \leq t)$

and,

$P(Y = X_1) = P(Y = X_2) = … = P(Y = X_n) = \frac{1}{n}.$

When $T(F)$ takes the form of an expectation with respect to $F$ , replacing $F$ with $\hat{F}_{n}$ yields,

$\hat{\theta} = T(\hat{F}_n) = \mathbb{E}_{\hat{F}_n}~g(Y).$

Since $\hat{F}_{n}$ is a discrete distribution,

$T(\hat{F}_n) = \sum_{i=1}^{n} g(X_i) P(Y = X_i)$

suggests that $T(\hat{F}_n)$ is just the sample average of the $n$ transformed $X_i$ ,

$T(\hat{F}_n) = \frac{1}{n} \sum_{i=1}^{n} g(X_i) .$

As an example, the sample expectation and variance can be easily expressed as plug-in estimators:

$\hat{\mu} = \mathbb{E}_{\hat{F}_n}[Y] = \sum_{i=1}^{n} X_i P(Y = X_i) = \frac{1}{n} \sum_{i=1}^{n} X_i = \bar{X}_{n}$

mu_hat = sum(1/n * X)
mu_hat

## [1] 5.245197

$\hat{\sigma}^{2} = \mathbb{E}_{\hat{F}_{n}}[(Y - \mathbb{E}_{\hat{F}_n}[Y])^2] = \mathbb{E}_{\hat{F}_n}[(X - \bar{X}_{n})^2] = \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar{X}_{n})^2.$

sigma2_hat = sum(1/n * (X - sum(1/n * X))^2)
sigma2_hat

## [1] 1.230199

Note that while $\bar{X}_{n}$ is the standard, unbiased estimator of the population mean, $\hat{\sigma}^{2}$ is the biased estimator of the population variance featuring a denominator of $n$ .

Not all empirical functionals, or plug-in estimators, are unbiased! However, when the statistical functional takes a special form, known as an expectation functional, an unbiased estimator can always be constructed regardless of the form of $F$ .

Download this blogpost as an RMarkdown file!

Expectation with respect to CDF

Empirical cumulative distribution function

Empirical functionals, or plug-in estimators

Published by

Emma Davies Smith

2 thoughts on “Plug-in estimators of statistical functionals”

Leave a Reply Cancel reply