
Review
Statistical functionals are any real-valued function of a distribution function ![]() ,
, ![]() . When
. When ![]() is unknown, nonparametric estimation only requires that
is unknown, nonparametric estimation only requires that ![]() belong to a broad class of distribution functions
belong to a broad class of distribution functions ![]() , typically subject only to mild restrictions such as continuity or existence of specific moments.
, typically subject only to mild restrictions such as continuity or existence of specific moments.
For a single independent and identically distributed random sample of size ![]() ,
, ![]() , a statistical functional
, a statistical functional ![]() is said to belong to the family of expectation functionals if:
is said to belong to the family of expectation functionals if:
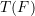 takes the form of an expectation of a function
takes the form of an expectation of a function 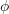 with respect to
with respect to 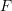 ,
,
![Rendered by QuickLaTeX.com \[T(F) = \mathbb{E}_F~ \phi(X_1, …, X_a) \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-4b10dae4aa2f3621fc36c4e99fec5e69_l3.png)
 is a symmetric kernel of degree
is a symmetric kernel of degree 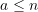 .
.
A kernel is symmetric if its arguments can be permuted without changing its value. For example, if the degree ![]() ,
, ![]() is symmetric if
is symmetric if ![]() .
.
If ![]() is an expecation functional and the class of distribution functions
is an expecation functional and the class of distribution functions ![]() is broad enough, an unbiased estimator of
is broad enough, an unbiased estimator of ![]() can always be constructed. This estimator is known as a U-statistic and takes the form,
can always be constructed. This estimator is known as a U-statistic and takes the form,
![]()
such that ![]() is the average of
is the average of ![]() evaluated at all
evaluated at all ![]() distinct combinations of size
distinct combinations of size ![]() from
from ![]() .
.
For more detail on expectation functionals and their estimators, check out my blog post U-, V-, and Dupree statistics.
Since each ![]() appears in more than one summand of
appears in more than one summand of ![]() , the central limit theorem cannot be used to derive the limiting distribution of
, the central limit theorem cannot be used to derive the limiting distribution of ![]() as it is the sum of dependent terms. However, clever conditioning arguments can be used to show that
as it is the sum of dependent terms. However, clever conditioning arguments can be used to show that ![]() is in fact asymptotically normal with mean
is in fact asymptotically normal with mean
![]()
and variance
![]()
where
![]()
The sketch of the proof is as follows:
- Express the variance of
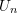 in terms of the covariance of its summands,
in terms of the covariance of its summands,
![Rendered by QuickLaTeX.com \[\text{Var}_{F}~ U_n = \frac{1}{{n \choose a}^2} \mathop{\sum \sum} \limits_{\substack{1 \leq i_1 < ... < i_{a} \leq n \\ 1 \leq j_1 < ... < j_{a} \leq n}} \text{Cov}\left[\phi(X_{i_1}, ..., X_{i_a}),~ \phi(X_{j_1}, ..., X_{j_a})\right].\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-a2c21d5d7f01714fd65d97bc9e5366a0_l3.png)
- Recognize that if two terms share
 common elements such that,
common elements such that,
![Rendered by QuickLaTeX.com \[ \text{Cov} [\phi(X_1, …, X_c, X_{c+1}, …, X_a), \phi(X_1, …, X_c, X'_{c+1}, …, X'_a)] \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-0afd7ad44b3d54edda4f587055601b06_l3.png)
conditioning on their
 shared elements will make the two terms independent.
shared elements will make the two terms independent. - For
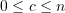 , define
, define
![Rendered by QuickLaTeX.com \[\phi_c(X_1, …, X_c) = \mathbb{E}_F \Big[\phi(X_1, …, X_a) | X_1, …, X_c \Big] \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-e5321ca7cbb2cc4e8035f405360737f8_l3.png)
such that
![Rendered by QuickLaTeX.com \[\mathbb{E}_F~ \phi_c(X_1, …, X_c) = \theta = T(F)\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-59b21c2f5cd533c3e54b99fef2e75a88_l3.png)
and
![Rendered by QuickLaTeX.com \[\sigma_{c}^2 = \text{Var}_{F}~ \phi_c(X_1, …, X_c).\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-5eae440995d70a60fcada6fcb85ecc89_l3.png)
Note that when
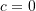 ,
, 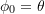 and
and 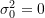 , and when
, and when  ,
, 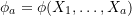 and
and 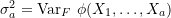 .
. - Use the law of iterated expecation to demonstrate that
![Rendered by QuickLaTeX.com \[ \sigma^{2}_c = \text{Cov} [\phi(X_1, …, X_c, X_{c+1}, …, X_a), \phi(X_1, …, X_c, X'_{c+1}, …, X'_a)] \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-ae2bc59e8a4485598141edc5f81b9a3d_l3.png)
and re-express
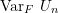 as the sum of the
as the sum of the 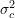 ,
,![Rendered by QuickLaTeX.com \[ \text{Var}_F~U_n = \frac{1}{{n \choose a}} \sum_{c=1}^{a} {a \choose c}{n-a \choose a-c} \sigma^{2}_c.\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-eeb9812359c7a08762e2d186b4ffecfd_l3.png)
Recognizing that the first variance term dominates for large
 , approximate
, approximate 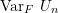 as
as![Rendered by QuickLaTeX.com \[\text{Var}_F~U_n \sim \frac{a^2}{n} \sigma^{2}_1.\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-2561ada44c52b7270d503a3b65cc4bdb_l3.png)
- Identify a surrogate
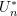 that has the same mean and variance as
that has the same mean and variance as 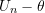 but is the sum of independent terms,
but is the sum of independent terms,
![Rendered by QuickLaTeX.com \[ U_n^{*} = \sum_{i=1}^{n} \mathbb{E}_F [U_n - \theta|X_i] \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-6279990329ef07296dfeb6bf7e3ff6ea_l3.png)
so that the central limit may be used to show
![Rendered by QuickLaTeX.com \[ \sqrt{n} U_n^{*} \rightarrow N(0, a^2 \sigma_1^2).\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-a5374b23424474a55f28fc80a9eca29d_l3.png)
- Demonstrate that
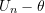 and
and 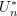 converge in probability,
converge in probability,
![Rendered by QuickLaTeX.com \[ \sqrt{n} \Big((U_n - \theta) - U_n^{*}\Big) \stackrel{P}{\rightarrow} 0 \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-03f17552990655c5c7bc7b2446eb452f_l3.png)
and thus have the same limiting distribution so that
![Rendered by QuickLaTeX.com \[\sqrt{n} (U_n - \theta) \rightarrow N(0, a^2 \sigma_1^2).\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-9e47c6463a7f5a734945b178bfc8dfad_l3.png)
For a walkthrough derivation of the limiting distribution of ![]() for a single sample, check out my blog post Getting to know U: the asymptotic distribution of a single U-statistic.
for a single sample, check out my blog post Getting to know U: the asymptotic distribution of a single U-statistic.
This blog post aims to provide an overview of the extension of kernels, expectation functionals, and the definition and distribution of U-statistics to multiple independent samples, with particular focus on the common two-sample scenario.
Continue reading Much Two U About Nothing: Extension of U-statistics to multiple independent samples
