Introduction
In a previous blogpost, I described how complex estimation of U-statistic variance can be simplified using a “structural component” approach introduced by Sen (1960). The structural component approach is very similar to the leave-one-out jackknife. Essentially, the idea behind both of these approaches is that we decompose the statistic into individual contributions. Here, these are referred to as “structural components,” and in the LOO jackknife, these are referred to as “pseudo-values” or sometimes “pseudo-observations.” Construction of these individual quantities differs conceptually somewhat, but in another blogpost, I discuss their one-to-one relationship for specific cases. We can then take the sample variance of these individual contributions to estimate the variance of the statistic.
Estimators for increasingly popular win measures, including the win probability, net benefit, win odds, and win ratio, are obtained using large-sample two-sample U-statistic theory. Variance estimators are complex for these measures, requiring the calculation of multiple joint probabilities.
Here, I demonstrate how variance estimation for win measures can be practically estimated in two-arm randomized trials using a structural component approach. Results and estimators are provided for the win probability, the net benefit, and the win odds. For simplicity, only a single outcome is considered. However, extension to hierarchical composite outcomes is immediate with use of an appropriate kernel function.
Setup
Consider a two-arm randomized trial that allocates ![]() individuals to the treatment arm and
individuals to the treatment arm and ![]() individuals to the control arm. Let
individuals to the control arm. Let ![]() represent the
represent the ![]() response in the treated arm, and
response in the treated arm, and ![]() represent the
represent the ![]() response in the control arm. Assume that responses are i.i.d. within each arm so
response in the control arm. Assume that responses are i.i.d. within each arm so ![]() and
and ![]() , and that greater responses are indicative of better health (e.g., HDL in cardiovascular disease, CD4 counts in infectious disease).
, and that greater responses are indicative of better health (e.g., HDL in cardiovascular disease, CD4 counts in infectious disease).
Win measures
Win measures rely on pairwise comparison of participants in two arms. That is, each treatment participant is compared to each control participant. Whoever responds better within a pair is the winner. If responses are the same, a tie occurs. Win measures tally wins, ties, and losses between trial arms to quantify treatment effects.
Win probability
In two-arm trials, the win probability is the probability that a randomly selected treated participant has a better response than a randomly selected control participant. Any ties are counted as half win and half loss, so the win probability is generally defined as:
(1) ![]()
![]() is framed in terms of the treatment participant responding better than the control participant, or a “treatment win,” so we refer to
is framed in terms of the treatment participant responding better than the control participant, or a “treatment win,” so we refer to ![]() as the “treatment win probability.” We could conversely frame
as the “treatment win probability.” We could conversely frame ![]() in terms of a “control win.” However, because a control win is a treatment loss, and vice versa, it follows that the control win probability is simply the complement of the treatment win probability:
in terms of a “control win.” However, because a control win is a treatment loss, and vice versa, it follows that the control win probability is simply the complement of the treatment win probability: ![]() .
.
![]() suggests that the probability that one participant responds better than the other is equal to the flip of a fair coin, or no treatment effect.
suggests that the probability that one participant responds better than the other is equal to the flip of a fair coin, or no treatment effect. ![]() suggests treatment wins more than expected by chance, or treatment benefit.
suggests treatment wins more than expected by chance, or treatment benefit. ![]() suggests treatment wins less than expected by chance, or treatment harm.
suggests treatment wins less than expected by chance, or treatment harm.
Net benefit
The net benefit, or perhaps “win difference,” is the difference between the treatment win probability and control win probability:
(2) ![]()
or equivalently, ![]() and
and ![]() . Ties cancel with differencing, so the net benefit also reduces to:
. Ties cancel with differencing, so the net benefit also reduces to:
(3) ![]()
For a single binary outcome with treatment and control success probabilities ![]() and
and ![]() , the net benefit is equal to the absolute risk difference:
, the net benefit is equal to the absolute risk difference:
(4) ![]()
![]() suggests the probability of winning is the same for both arms,
suggests the probability of winning is the same for both arms, ![]() suggests treatment benefit, and
suggests treatment benefit, and ![]() suggests treatment harm.
suggests treatment harm.
Win odds
The win odds is the ratio of the treatment win probability to the control win probability:
(5) ![]()
or equivalently, ![]() Estimators for the win probability can be translated to the win odds through use of the
Estimators for the win probability can be translated to the win odds through use of the ![]() -method.
-method.
![]() represents treatment wins:losses, so
represents treatment wins:losses, so ![]() suggests no treatment effect,
suggests no treatment effect, ![]() suggests treatment benefit, and
suggests treatment benefit, and ![]() suggests treatment harm.
suggests treatment harm.
Two-sample U-statistic theory
Win measures are estimated by comparing all pairs consisting of one treatment response and one control response. In this case, there are ![]() such pairs. A score is assigned to each pair depending on whether it is a treatment win, tie, or loss. Using different scoring systems will result in estimates of different win measures. The mean of these scores provides a point estimate of the win measure.
such pairs. A score is assigned to each pair depending on whether it is a treatment win, tie, or loss. Using different scoring systems will result in estimates of different win measures. The mean of these scores provides a point estimate of the win measure.
You might recognize that this point estimator is a U-statistic! Yes indeed, estimators of the net benefit and win probability take the form of two-sample U-statistics:
(6) 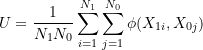
where ![]() is a valid two-sample kernel function.
is a valid two-sample kernel function.
For the win probability,
(7) ![]()
where ![]() is an indicator function taking the value 1 when its argument is true and 0 otherwise.
is an indicator function taking the value 1 when its argument is true and 0 otherwise. ![]() assigns a score of +1 to treatment wins (control losses), +0.5 to ties, and 0 to treatment losses (control wins).
assigns a score of +1 to treatment wins (control losses), +0.5 to ties, and 0 to treatment losses (control wins).
For the net benefit,
(8) ![]()
![]() assigns a score of +1 to treatment wins (control losses), +0 to ties, and -1 to treatment losses (control wins).
assigns a score of +1 to treatment wins (control losses), +0 to ties, and -1 to treatment losses (control wins).
Large-sample theory provides the variance for two-sample U-statistics of this general form,
(9) ![]()
The variance components ![]() and
and ![]() are the cause of all pain in variance estimation! The form of
are the cause of all pain in variance estimation! The form of ![]() results from Hoeffding decomposition, which I won’t go into detail about here. The basic idea is that the U-statistic can be split into multiple uncorrelated terms. The variance of these terms provides the variance equation you see above (after the asymptotic zeroing of higher-order terms).
results from Hoeffding decomposition, which I won’t go into detail about here. The basic idea is that the U-statistic can be split into multiple uncorrelated terms. The variance of these terms provides the variance equation you see above (after the asymptotic zeroing of higher-order terms).
If we take the expectation of the kernel ![]() conditional on
conditional on ![]() , the resulting quantity is independent of
, the resulting quantity is independent of ![]() . This is because when we condition on a quantity, we treat it as fixed (constant). For a generic kernel function, let’s define these quantities for each arm:
. This is because when we condition on a quantity, we treat it as fixed (constant). For a generic kernel function, let’s define these quantities for each arm:
(10) ![]()
and
(11) ![]()
Because the ![]() and
and ![]() are i.i.d. within their respective arm, it follows that
are i.i.d. within their respective arm, it follows that ![]() and
and ![]() are similarly i.i.d. The variance components are then provided by
are similarly i.i.d. The variance components are then provided by ![]() and
and ![]() .
.
I’ve figured out the exact form of these variance components for specific U-statistics in previous blog posts. It’s really tricky, even for what you might expect are “simple” U-statistics!!!
Finally, U-statistic ![]() is unbiased and asymptotically normal with mean
is unbiased and asymptotically normal with mean ![]() and variance
and variance ![]() . Here,
. Here, ![]() or
or ![]() depending on the kernel used. This provides your classic large-sample 95% confidence interval estimator,
depending on the kernel used. This provides your classic large-sample 95% confidence interval estimator,
(12) ![]()
Replace 1.96 with your favourite critical value!
Variance estimation via U-statistic structural components
As outlined in a previous blogpost, Sen (1960) teaches us that we can avoid the pain of variance estimation in two steps: (1) TRANSFORM observed responses ![]() and
and ![]() into structural components. Structural components are constructed as the within-subject mean of the
into structural components. Structural components are constructed as the within-subject mean of the ![]() corresponding kernel values or “scores,” converge in probability to the quantities
corresponding kernel values or “scores,” converge in probability to the quantities ![]() and
and ![]() , and are approximately uncorrelated in large samples; (2) ESTIMATE the sample variance of the structural components to obtain
, and are approximately uncorrelated in large samples; (2) ESTIMATE the sample variance of the structural components to obtain ![]()
In the following sections, I demonstrate how to apply these results to obtain practical variance estimators for the win probability, net benefit, and win odds. Then, I generate data and demonstrate their application.
Win probability and win odds
For the win probability, the ![]() treated structural component corresponding to observed response
treated structural component corresponding to observed response ![]() is defined as,
is defined as,
(13) ![]()
or the mean of the ![]() scores resulting from pairwise comparison of
scores resulting from pairwise comparison of ![]() . Again,
. Again, ![]() approximates
approximates ![]() , or the expected value of the kernel conditional on
, or the expected value of the kernel conditional on ![]() . Similarly, the
. Similarly, the ![]() control structural component corresponding to observed response
control structural component corresponding to observed response ![]() is defined as,
is defined as,
(14) ![]()
which approximates ![]() , or the expected value of the kernel conditional on
, or the expected value of the kernel conditional on ![]() .
.
Notice that the mean of the treated structural components ![]() ,
,
(15) ![]()
or the control structural components ![]() ,
,
(16) ![Rendered by QuickLaTeX.com \begin{equation*} \bar{W}_{0.} = \frac{1}{N_0} \sum_{j=1}^{N_0} \left[ \frac{1}{N_1} \sum_{i=1}^{N_1} \phi_{\theta}(X_{1i}, X_{0j}) \right] \end{equation*}](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-dbe41ca75fe2cb8c525ec7f8968c868b_l3.png)
equals the U-statistic estimator of the win probability ![]() ,
,
(17) 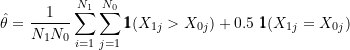
and by definition ![]() .
.
We take advantage of the fact that ![]() and
and ![]() approximate the
approximate the ![]() and
and ![]() (and are asymptotically uncorrelated), by taking their sample variance to approximate the required variance components
(and are asymptotically uncorrelated), by taking their sample variance to approximate the required variance components ![]() and
and ![]() :
:
(18) ![]()
and
(19) 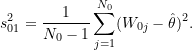
Then, an estimator of ![]() is obtained as,
is obtained as,
(20) ![]()
We can also obtain a variance estimator for the win odds, ![]() by applying the
by applying the ![]() -method:
-method:
(21) ![]()
Net benefit
For the net benefit, the ![]() treated structural component corresponding to observed response
treated structural component corresponding to observed response ![]() is defined as,
is defined as,
(22) ![]()
or the mean of the ![]() scores resulting from pairwise comparison of
scores resulting from pairwise comparison of ![]() . Again,
. Again, ![]() approximates
approximates ![]() , or the expected value of the kernel conditional on
, or the expected value of the kernel conditional on ![]() . Similarly, the
. Similarly, the ![]() control structural component corresponding to observed response
control structural component corresponding to observed response ![]() is defined as,
is defined as,
(23) ![]()
which approximates ![]() , or the expected value of the kernel conditional on
, or the expected value of the kernel conditional on ![]() .
.
Notice that the mean of the treated structural components ![]() ,
,
(24) ![]()
or the control structural components ![]() ,
,
(25) ![Rendered by QuickLaTeX.com \begin{equation*} \bar{D}_{0.} = \frac{1}{N_0} \sum_{j=1}^{N_0} \left[ \frac{1}{N_1} \sum_{i=1}^{N_1} \phi_{\Delta}(X_{1i}, X_{0j}) \right] \end{equation*}](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-3299d85ec49307545d053d1c144706bb_l3.png)
equals the U-statistic estimator of the net benefit ![]() ,
,
(26) 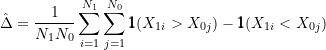
and by definition ![]() .
.
We take advantage of the fact that ![]() and
and ![]() approximate the
approximate the ![]() and
and ![]() (and are asymptotically uncorrelated), by taking their sample variance to approximate the required variance components
(and are asymptotically uncorrelated), by taking their sample variance to approximate the required variance components ![]() and
and ![]() :
:
(27) ![]()
and
(28) 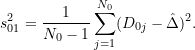
Then, an estimator of ![]() is obtained as,
is obtained as,
(29) ![]()
Notice that because ![]() , analogous to the relationship between the net benefit and win probability,
, analogous to the relationship between the net benefit and win probability, ![]() .
.
Simulated examples
Variance estimation using structural components can be performed with a few lines of code in R and SAS. We generate a single binary outcome measure according to a fixed value of the win probability, and obtain point and variance estimates of the win probability, the win odds, and the net benefit using the methods described above.
Let ![]() and
and ![]() . In this special case, the net benefit
. In this special case, the net benefit ![]() and it follows that the win probability
and it follows that the win probability ![]() . Fixing
. Fixing ![]() suggests that
suggests that ![]() to obtain win probability
to obtain win probability ![]() and
and ![]() .
.
# Event probability (1=treated, 0=control)
Pi1 = 0.5
Pi0 = 0.22
# Function to calculate win probability given Pi1, Pi0
Theta <- function(Pi1, Pi0){ (Pi1-Pi0+1)/2 }
# Function to calculate net benefit given Pi1, Pi0
Delta <- function(Pi1, Pi0){ (Pi1-Pi0) }
# Function to calculate win odds given Pi1, Pi0
Lambda <- function(Pi1, Pi0){ (1+(Pi1-Pi0))/(1-(Pi1-Pi0)) }
# True value of win probability
Theta(Pi1, Pi0)
## [1] 0.64
# True value of net benefit
Delta(Pi1, Pi0)
## [1] 0.28
# True value of win odds
Lambda(Pi1, Pi0)
## [1] 1.777778
Independently and identically generate ![]() binary responses for each arm, corresponding perfect 1:1 randomization of 200 total participants.
binary responses for each arm, corresponding perfect 1:1 randomization of 200 total participants.
# Sample size (1=treated, 0=control)
N1 = 100
N0 = 100
# Set seed!!!
set.seed(12345)
# Generate i.i.d. response in each arm
# X1i ~ Binomial(n=1, Pi1)
# X0j ~ Binomial(n=1, Pi0)
X1 <- rbinom(n=N1, size=1, prob=Pi1)
X0 <- rbinom(n=N0, size=1, prob=Pi0)
# Event (1) and non-event (0) in treated arm
prop.table(table(X1))
## X1 ## 0 1 ## 0.48 0.52
# Event (1) and non-event (0) in control arm
prop.table(table(X0))
## X0 ## 0 1 ## 0.67 0.33
Win probability
First, lets construct the kernel function for the win probability.
# Win Probability = Pr(X1i > X0j) + 0.5 Pr(X1i = X0j)
# kernel function for win probability Theta
kTheta <- function(X1i, X0j){ ifelse(X1i > X0j, 1, 0) + 0.5 * ifelse(X1i == X0j, 1, 0) }
# Treatment Win
kTheta(X1i=1, X0j=0)
## [1] 1
# Tie
kTheta(X1i=1, X0j=1)
## [1] 0.5
# Tie
kTheta(X1i=0, X0j=0)
## [1] 0.5
# Treatment Loss
kTheta(X1i=0, X0j=1)
## [1] 0
Second, lets use the kernel to score or compare all treatment and control participant pairs.
# Matrix to store scores (kernel values) for each participant pair
# row = treated participant
# column = control participant
kMatrix <- matrix(NA, nrow=N1, ncol=N0)
# Double loop to compute and store all kernel values
for (i in 1:N1){
for (j in 1:N0){
kMatrix[i, j] = kTheta(X1[i], X0[j])
}
}
Third, construct the treated structural components as the row means and control structural components as the column means.
W1i <- 1/N0 * rowSums(kMatrix)
W0j <- 1/N1 * colSums(kMatrix)
The means of the structural components should be the same between-arms:
# Treatment Win probability = Mean(Treated Structural Components)
theta = mean(W1i)
theta
## [1] 0.595
# Treatment Win probability = Mean(Control Structural Components)
theta = mean(W0j)
theta
## [1] 0.595
and represent our point estimate of the win probability! That is, ![]() 0.595. Recall true
0.595. Recall true ![]() 0.64.
0.64.
Third, the variance is easily estimated by taking the sample variances of W1i and W0j:
# First variance component, V10=Var[E[K(X1i, X0j) | X1i]]
var10W <- var(W1i)
var10W
## [1] 0.0630303
# Second variance component, V01=Var[E[K(X1i, X0j) | X0j]]
var01W <- var(W0j)
var01W
## [1] 0.05583333
# V(hat(Theta)) = V10(W1j)/N1 + V01(W0j)/N0
vartheta <- var10W/N1 + var01W/N0
vartheta
## [1] 0.001188636
Finally, the large-sample 95% confidence interval for the win probability:
wlower = theta - 1.96 * sqrt(vartheta)
wupper = theta + 1.96 * sqrt(vartheta)
c(wlower, wupper)
## [1] 0.5274259 0.6625741
The null win probability ![]() is not contained within the 95% confidence interval, suggesting there is a statistically significant difference between arms at the 5% level. The point estimate
is not contained within the 95% confidence interval, suggesting there is a statistically significant difference between arms at the 5% level. The point estimate ![]() 0.595 suggests that a random treated participant will have a better response than (win over) a random control participant 59.5% of the time (technically with adjustment for ties). The bounds suggest win probabilities as low as 52.7% and as high as 66.3% are compatible with the data. The true value of the win probability
0.595 suggests that a random treated participant will have a better response than (win over) a random control participant 59.5% of the time (technically with adjustment for ties). The bounds suggest win probabilities as low as 52.7% and as high as 66.3% are compatible with the data. The true value of the win probability ![]() 0.64 is contained within the interval.
0.64 is contained within the interval.
Win odds
We can transform win probability results to the win odds:
# Win Odds = Treatment Win Probability / Treatment Loss Probability
# Lambda = Theta/(1-Theta)
lambda = theta/(1-theta)
lambda
## [1] 1.469136
# Take the log for delta method
lnlambda = log(lambda)
lnlambda
## [1] 0.3846743
Then apply the ![]() -method to
-method to ![]() to obtain a variance estimator for confidence interval construction.
to obtain a variance estimator for confidence interval construction.
# Calculate variance according to delta method result
varlambda = vartheta / (theta*(1-theta))^2
varlambda
## [1] 0.0204694
Construct the 95% confidence interval first on the log scale,
lnlower = lnlambda - 1.96 * sqrt(varlambda)
lnupper = lnlambda + 1.96 * sqrt(varlambda)
c(lnlower, lnupper)
## [1] 0.1042546 0.6650941
then back-transform the confidence interval to the original scale,
c(exp(lnlower), exp(lnupper))
## [1] 1.109883 1.944673
The null win odds ![]() is not contained within the 95% confidence interval, suggesting there is a statistically significant difference between arms at the 5% level. The point estimate
is not contained within the 95% confidence interval, suggesting there is a statistically significant difference between arms at the 5% level. The point estimate ![]() 1.47 suggests that the treatment win probability is 47% greater (relative) than the control win probability. The bounds suggest win odds as low as 1.11 and as high as 1.94 are compatible with the data. The true value of the win odds
1.47 suggests that the treatment win probability is 47% greater (relative) than the control win probability. The bounds suggest win odds as low as 1.11 and as high as 1.94 are compatible with the data. The true value of the win odds ![]() 1.78 is contained within the interval.
1.78 is contained within the interval.
Net benefit
First of all, we can also get estimates of the net benefit using the win probability by recognizing that ![]() ,
,
# Net Benefit = Treatment Win Probability - Control Win Probability
# Net Benefit = 2 * Treatment Win Probability - 1
delta = 2 * theta - 1
delta
## [1] 0.19
and subsequently ![]() ,
,
vardelta = 4 * vartheta
vardelta
## [1] 0.004754545
and construct a 95% confidence interval for ![]() ,
,
dlower = delta - 1.96 * sqrt(vardelta)
dupper = delta + 1.96 * sqrt(vardelta)
c(dlower, dupper)
## [1] 0.0548517 0.3251483
Though you can just as easily apply the same transform to the 95% confidence interval bounds for ![]() …
…
2*c(wlower, wupper)-1
## [1] 0.0548517 0.3251483
But, lets also do the structural component approach the long way for good measure! We are all about good measure here.
First, lets construct the kernel function for the net benefit,
# Net Benefit = Pr(X1i > X0j) - Pr(X1i < X0j)
# kernel function for net benefit Delta
kDelta <- function(X1i, X0j){ ifelse(X1i > X0j, 1, 0) - ifelse(X1i < X0j, 1, 0) }
# Treatment Win
kDelta(X1i=1, X0j=0)
## [1] 1
# Tie
kDelta(X1i=1, X0j=1)
## [1] 0
# Tie
kDelta(X1i=0, X0j=0)
## [1] 0
# Treatment Loss
kDelta(X1i=0, X0j=1)
## [1] -1
Second, lets use the kernel to score or compare all treatment and control participant pairs.
# Matrix to store scores (kernel values) for each participant pair
# row = treated participant
# column = control participant
kMatrix <- matrix(NA, nrow=N1, ncol=N0)
# Double loop to compute and store all kernel values
for (i in 1:N1){
for (j in 1:N0){
kMatrix[i, j] = kDelta(X1[i], X0[j])
}
}
Third, construct the treated structural components as the row means and control structural components as the column means.
D1i <- 1/N0 * rowSums(kMatrix)
D0j <- 1/N1 * colSums(kMatrix)
The means of the structural components should be the same between-arms:
# Net Benefit = Mean(Treated Structural Components)
delta = mean(D1i)
delta
## [1] 0.19
# Net Benefit = Mean(Control Structural Components)
delta = mean(D0j)
delta
## [1] 0.19
and represent our point estimate of the net benefit! That is, ![]() 0.595. Recall true
0.595. Recall true ![]() 0.28.
0.28.
Third, the variance is easily estimated by taking the sample variances of D1i and D0j:
# First variance component, V10=Var[E[K(X1i, X0j) | X1i]]
var10D <- var(D1i)
var10D
## [1] 0.2521212
# Second variance component, V01=Var[E[K(X1i, X0j) | X0j]]
var01D <- var(D0j)
var01D
## [1] 0.2233333
# V(hat(Delta)) = V10(D1j)/N1 + V01(D0j)/N0
vardelta <- var10D/N1 + var01D/N0
vardelta
## [1] 0.004754545
Finally, the large-sample 95% confidence interval for the net benefit:
dlower = delta - 1.96 * sqrt(vardelta)
dupper = delta + 1.96 * sqrt(vardelta)
c(dlower, dupper)
## [1] 0.0548517 0.3251483
Same as before, far out!
The null net benefit ![]() is not contained within the 95% confidence interval, suggesting there is a statistically significant difference between arms at the 5% level. The point estimate
is not contained within the 95% confidence interval, suggesting there is a statistically significant difference between arms at the 5% level. The point estimate ![]() 0.19 suggests that the treatment win probability is 19% greater (absolute) than the control win probability. The bounds suggest net benefits as low as 5% and as high as 33% are compatible with the data. The true value of the net benefit
0.19 suggests that the treatment win probability is 19% greater (absolute) than the control win probability. The bounds suggest net benefits as low as 5% and as high as 33% are compatible with the data. The true value of the net benefit ![]() 0.28 is contained within the interval.
0.28 is contained within the interval.
Confidence interval coverage
Just for fun, let’s repeat this process 1,000 times for specifically the win probability and sample sizes ![]() ,
, ![]() , and
, and ![]() to assess estimator performance in smaller and larger samples with respect to 95% confidence interval coverage.
to assess estimator performance in smaller and larger samples with respect to 95% confidence interval coverage.
N <- c(10, 30, 100)
B <- 1000
Results <- cbind('n'=NA, 'b'=NA, 'theta'=NA, 'wlower'=NA, 'wupper'=NA, 'cover'=NA)
# for each of 3 sample sizes
for (i in 1:3){
n <- N[i]
# for each of 1000 replicates
for (b in 1:B){
# generate binary responses
X1 <- rbinom(n=n, size=1, prob=Pi1)
X0 <- rbinom(n=n, size=1, prob=Pi0)
# Double loop to compute and store all kernel values
kMatrix <- matrix(NA, nrow=n, ncol=n)
for (i in 1:n){
for (j in 1:n){
kMatrix[i, j] = kTheta(X1[i], X0[j])
}
}
# Construct structural components
W1i <- 1/n * rowSums(kMatrix)
W0j <- 1/n * colSums(kMatrix)
# Estimate win probability (using treatment structural components)
theta = mean(W1i)
# First variance component, V10=Var[E[K(X1i, X0j) | X1i]]
var10W <- var(W1i)
# Second variance component, V01=Var[E[K(X1i, X0j) | X0j]]
var01W <- var(W0j)
# V(hat(Theta)) = V10(W1j)/N1 + V01(W0j)/N0
vartheta <- var10W/N1 + var01W/N0
# Build confidence intervals and check coverage
# wlower = lower bound of 95% confidence interval
# wupper = upper bound of 95% confidence interval
# cover = 1 if truth Theta in confidence bounds
wlower = theta - 1.96 * sqrt(vartheta)
wupper = theta + 1.96 * sqrt(vartheta)
clower = (wlower < Theta(Pi1, Pi0))
cupper = (wupper > Theta(Pi1, Pi0))
cover = clower*cupper
# Store replicate result
result <- c(n, b, theta, wlower, wupper, cover)
Results <- rbind(Results, result)
}
}
# Remove first row of NAs from Results
Results <- data.frame(Results[-1,])
Now lets look at the results by sample size!
# Simulation results when N1=N0=10
round(colMeans(Results[Results$n==10,]), 2)
## n b theta wlower wupper cover ## 10.00 500.50 0.64 0.58 0.71 0.53
# Simulation results when N1=N0=30
round(colMeans(Results[Results$n==30,]), 2)
## n b theta wlower wupper cover ## 30.00 500.50 0.64 0.57 0.70 0.75
# Simulation results when N1=N0=100
round(colMeans(Results[Results$n==100,]), 2)
## n b theta wlower wupper cover ## 100.00 500.50 0.64 0.58 0.70 0.95
First, they confirm our estimator is unbiased. We see that coverage is conservative when there is ![]() participants in each arm, with only ~50% of 95% confidence containing the true value of
participants in each arm, with only ~50% of 95% confidence containing the true value of ![]() 0.64. However, coverage increases to the expected 95% when
0.64. However, coverage increases to the expected 95% when ![]() . Results for
. Results for ![]() fall somewhere in between.
fall somewhere in between.
Summary
In summary, decomposing U-statistics into their arm-specific structural components improves the practicality of variance estimation significantly. All one has to do is take the within-subject mean of the kernel to obtain structural components for all participants. The within-arm sample variance of the structural components can then be used to approximate the variance of the U-statistic. These steps are much easier to accomplish than parsing and implementing complex joint probabilities!!! You just need to know the correct kernel. The methods described here are extremely flexible, and can also be applied to U-statistics outside the realm of win measures.
An important thing to remember is that all these results depend on LARGE SAMPLES. That is, the form of the variance estimator is based on asymptotic zeroing of higher order terms, and validity of the sample variance estimators depends on the structural components being asymptotically uncorrelated. Because construction of the structural components shares the same sample observations, they have non-negligible correlation in small samples, which will result in biased variance estimates. We saw this in our simulation study. However, it has been proven that the variance will always be conservatively biased, and we emphasize that this bias is mitigated as sample sizes increase.
The fact that all these measures are connected to each other and other popular treatment effects, and yet all have their own pros and cons, is cool to me. They definitely do work well together. It’s fun how estimators for the net benefit and win odds can be recovered from the win probability. The variance of the win ratio is a bit trickier to estimate because it excludes ties, so we can’t use this same trick. Its ratio form means it also does not have a nice linear kernel like the win probability or net benefit. Neither does the win odds, but its relationship with the win probability provides estimators. The current method uses two U-statistics, one for the numerator and one for the denominator, and then take their ratio on an appropriate scale. In this case, multivariate, or at least bivariate, U-statistic theory is needed. Makes sense to me… I wonder if this could be used to simplify calculation of covariances.
I hope this makes your life just a little bit easier, and thanks for reading my blog!

P.S. So tempted to name this “Practical magic for win measures”…