The Probabilistic Index for Two Normally Distributed Outcomes

Consider a two-armed study comparing a placebo and treatment. In general, the probabilistic index (PI) is defined as,

$\text{PI} = P(X < Y) + \frac{1}{2} P(X = Y)$

and is interpreted as the probability that a subject in the treatment group will have an increased response compared to a subject in the placebo group. The probabilistic index is a particularly useful effect measure for ordinal data, where effects can be difficult to define and interpret owing to absence of a meaningful difference. However, it can also be used for continuous data, noting that when the outcome is continuous, $P(X = Y) = 0$ and the PI reduces to $P(X < Y)$ .

$PI = 0.5$ suggests an increased outcome is equally likely for subjects in the placebo and treatment group, while $PI > 0.5$ suggests an increased outcome is more likely for subjects in the treatment group compared to the placebo group, and the opposite is true when $PI < 0.5$ .

Simulation

Suppose $X \sim N(\mu_X, \sigma^{2}_{X})$ and $Y \sim N(\mu_Y, \sigma^{2}_{Y})$ represent the independent outcomes in the placebo and treatment groups, respectively and an increased value of the outcome is the desired response.

We simulate $n_X = n_Y = 50$ observations from each group such that treatment truly increases the outcome and the variances within each group are equal such that $\sigma^{2}_{X} = \sigma^{2}_{Y}$ .

# Loading required libraries
library(tidyverse)
library(gridExtra)

# Setting seed for reproducibility
set.seed(12345)

# Simulating data
n_X = n_Y = 50
sigma_X = sigma_Y = 1
mu_X = 5; mu_Y = 7

outcome_X = rnorm(n = n_X, mean = mu_X, sd = sigma_X)
outcome_Y = rnorm(n = n_Y, mean = mu_Y, sd = sigma_Y)

df <- data.frame(Group = c(rep('Placebo', n_X), rep('Treatment', n_Y)),
                 Outcome = c(outcome_X, outcome_Y))

Examining side-by-side histograms and boxplots of the outcomes within each group, there appears to be strong evidence that treatment increases the outcome as desired. Thus, we would expect a probabilistic index close to 1 as most outcomes in the treatment group appear larger than those of the placebo group.

# Histogram by group
hist_p <- df %>%
  ggplot(aes(x = Outcome, fill = Group)) +
    geom_histogram(position = 'identity', alpha = 0.75, bins = 10) + 
    theme_bw() +
    labs(y = 'Frequency')

# Boxplot by group
box_p <- df %>%
  ggplot(aes(x = Outcome, fill = Group)) +
    geom_boxplot() + 
    theme_bw() +
    labs(y = 'Frequency')

# Combine plots
grid.arrange(hist_p, box_p, nrow = 2)

plot of chunk unnamed-chunk-3

Estimation

To estimate the probabilistic index in this scenario, we need to:

Construct all 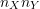$n_X n_Y$ possible pairs of treatment and placebo subjects.
Within each placebo-treatment subject pair, compare their outcomes to determine which group had the “better” (larger) response.
Count the number of pairs for which the treatment group had a “better” response, referred to as “wins”. Note that our outcome is normally distributed (i.e. continuous) and recorded with sufficient decimal places to prevent ties in our scenario.
Divide the number of wins by the total number of pairs evaluated to obtain an estimate of the probabilistic index.

# Create all placebo-treatment subject pairs
# Take the difference of their outcomes: (placebo - treatment)
pairs <- outer(X = df$Outcome[df$Group == 'Placebo'], 
               Y = df$Outcome[df$Group == 'Treatment'],  
               FUN = "-")

# If difference < 0, treatment subj. had greater outcome
# If difference = 0, treatment subj. had same outcome (not possible here)
# If difference > 0, treatment subj. had lesser outcome
treat_wins <- sum(ifelse(pairs < 0, 1, 0))

# Eetimate P(Y < X)
PI_YX <- treat_wins / (n_X * n_Y)
PI_YX

## [1] 0.9144

There were 2286 placebo-treatment subject pairs for which treatment yielded a greater outcome than placebo, or 2286 wins for the treatment group. Dividing this by the total number of pairs, the estimated probabilistic index $P(X < Y)$ is 0.9144, suggesting that there is a 91.4% chance that a patient receiving treatment will have a greater, or better, outcome compared to a patient receiving placebo.

Alternatively, the probabilistic index is equivalent to the Wilcoxon Mann-Whitney $U$ -statistic,

$U = \frac{1}{n_X n_Y} \sum_{i=1}^{n_X} \sum_{j=1}^{n_Y} I(X_i < Y_j)$

so we can use R’s built-in WMW test, wilcox.test, to calculate it for us.

Here, the test statistic $W$ is equal to the number of pairs for which the placebo outcome is greater than the treatment outcome, i.e. $Y < X$ . Thus, we can estimate the PI we are looking for by dividing this value by the total number of pairs and subtracting it from 1 as $P(X < Y) = 1 - P(Y < X).$

wt <- wilcox.test(Outcome ~ Group, data = df)
wt

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  Outcome by Group
## W = 214, p-value = 9.432e-13
## alternative hypothesis: true location shift is not equal to 0

placebo_wins <- wt$statistic

# P(Y < X)
PI_XY <- placebo_wins / (n_X * n_Y)

# P(X < Y) = 1 - P(Y < X)
PI_YX <- 1 - PI_XY

The number of pairs for which the placebo outcome is greater than the treatment outcome is W = 214. Dividing by the total number of pairs, the probabilistic index $P(X < Y) = 1 - P(Y < X)$ is once again estimated as 0.9144.

Relationship between Probabilistic Index & Cohen’s Effect Size

Cohen’s effect size attempts to capture effects on both the mean and variance by standardizing the difference in means by the pooled standard deviation such that,

$\delta = \frac{\mu_Y - \mu_X}{\sqrt{\frac{1}{2}(\sigma^2_Y + \sigma^2_X)}}.$

When outcomes are normally distributed, it can be shown that

$P(X < Y) = \Phi \left[ \frac{\mu_{Y} - \mu_{X}}{\sqrt{\sigma_{X}^2 + \sigma_{Y}^2}}\right] = \Phi \left[ \frac{\delta}{\sqrt{2}}\right].$

Thus, we can plug in our chosen parameters $\mu_X$ , $\mu_Y$ , $\sigma_X$ , and $\sigma_Y$ from our simulation to obtain the true value of the PI.

delta = (mu_Y - mu_X) / sqrt(0.5 * (sigma_X^2 + sigma_Y^2))
PI_param = pnorm(delta / sqrt(2))

Here, the true PI is 0.9214 which is quite close to our sample estimate 0.9144.

Cohen’s effect size captures both differences in location and scale, similar to the probabilistic index, but can be more challenging to interpret. An effect size $\delta$ suggests that the mean outcome in the treatment group is $\delta$ standard deviations lower than the placebo group.

Standard deviations as units are not typically tangible for practitioners, so Cohen proposed guidelines for judging effect sizes based on $\delta$ . $\delta = 0.2$ suggests a small effect size, $\delta = 0.5$ a medium effect size, and $\delta = 0.8$ a large effect size. In our simulated scenario, the treatment effect would be considered “large”, as expected. However, Cohen’s guidelines were based on the assumption that outcomes in each group are normally distributed data with equal variances. When these assumptions are not met, for example when distributions are skewed or variances are unequal, these rules of thumb may not be appropriate.

The probabilistic index provides a simple interpretation free of these assumptions. Furthermore, the probabilistic index is invariant to monotone (or order-preserving) transformations such as the log, exponential, and inverse transforms. That is, for example, $P(\log X < \log Y) = P(X < Y).$ Unfortunately, when there is minimal overlap between the group distributions, the PI will be approximately 1 regardless of the separation between the groups and therefore uninformative. On the other hand, Cohen’s effect size will reflect a difference in groups in such a scenario. For both metrics, however, its important to note that a difference in variances can mask a difference in means.

Simulation

Estimation

Relationship between Probabilistic Index & Cohen’s Effect Size

Published by

Emma Davies Smith

One thought on “The Probabilistic Index for Two Normally Distributed Outcomes”

Leave a Reply Cancel reply