After my last grand slam title, U-, V-, and Dupree statistics I was really feeling the pressure to keep my title game strong. Thank you to my wonderful friend Steve Lee for suggesting this beautiful title.
Overview
A statistical functional is any real-valued function of a distribution function 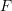 such that
such that
![Rendered by QuickLaTeX.com \[ \theta = T(F) \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-a075386bce98362038162a77be947177_l3.png)
and represents characteristics of the distribution 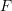 and include the mean, variance, and quantiles.
and include the mean, variance, and quantiles.
Often times 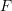 is unknown but is assumed to belong to a broad class of distribution functions
is unknown but is assumed to belong to a broad class of distribution functions 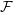 subject only to mild restrictions such as continuity or existence of specific moments.
subject only to mild restrictions such as continuity or existence of specific moments.
A random sample 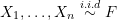 can be used to construct the empirical cumulative distribution function (ECDF)
can be used to construct the empirical cumulative distribution function (ECDF) 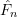 ,
,
![Rendered by QuickLaTeX.com \[ \hat{F}_{n}(x) = \frac{1}{n} \sum_{i=1}^{n} \mathbb{I}(X_i \leq x) \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-a40fd6ad512cfdc60816cc7fd6757918_l3.png)
which assigns mass  to each
to each 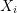 .
.
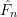 is a valid, discrete CDF which can be substituted for
is a valid, discrete CDF which can be substituted for 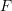 to obtain
to obtain 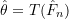 . These estimators are referred to as plug-in estimators for obvious reasons.
. These estimators are referred to as plug-in estimators for obvious reasons.
For more details on statistical functionals and plug-in estimators, you can check out my blog post Plug-in estimators of statistical functionals!
Many statistical functionals take the form of an expectation of a real-valued function 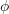 with respect to
with respect to 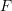 such that for
such that for 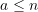 ,
,
![Rendered by QuickLaTeX.com \[ \theta = T(F) = \mathbb{E}_{F}~ \phi(X_1, …, X_a) .\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-c9113700df3aa7ec132bbc5ce1dd5066_l3.png)
When  is a function symmetric in its arguments such that, for e.g.
is a function symmetric in its arguments such that, for e.g. 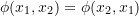 , it is referred to as a symmetric kernel of degree
, it is referred to as a symmetric kernel of degree  . If
. If 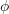 is not symmetric, a symmetric equivalent
is not symmetric, a symmetric equivalent 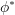 can always be found,
can always be found,
![Rendered by QuickLaTeX.com \[\phi^{*}(x_1, …, x_a) = \frac{1}{a!} \sum_{\pi ~\in~ \Pi} \phi(x_{\pi(1)}, …, x_{\pi(a)})\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-d152c08716f0530e6b97232c5dc3061a_l3.png)
where  represents the set of all permutations of the indices
represents the set of all permutations of the indices  .
.
A statistical functional 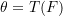 belongs to a special family of expectation functionals when:
belongs to a special family of expectation functionals when:
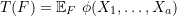 , and
, and is a symmetric kernel of degree
is a symmetric kernel of degree  .
.
Plug-in estimators of expectation functionals are referred to as V-statistics and can be expressed explicitly as,
![Rendered by QuickLaTeX.com \[V_n = \frac{1}{n^a} \sum_{i_1 = 1}^{n} … \sum_{i_a = 1}^{n} \phi(X_{i_1}, …, X_{i_a}) \]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-f17242e846aca4ec7a693f1d2bfaacf8_l3.png)
so that  is the average of
is the average of  evaluated at all possible permutations of size
evaluated at all possible permutations of size  from
from  . Since the
. Since the 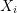 can appear more than once within each summand,
can appear more than once within each summand, 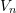 is generally biased.
is generally biased.
By restricting the summands to distinct indices only an unbiased estimator known as a U-statistic arises. In fact, when the family of distributions 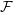 is large enough, it can be shown that a U-statistic can always be constructed for expectation functionals.
is large enough, it can be shown that a U-statistic can always be constructed for expectation functionals.
Since 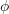 is symmetric, we can require that
is symmetric, we can require that  , resulting in
, resulting in 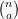 combinations of the subscripts
combinations of the subscripts 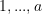 . The U-statistic is then the average of
. The U-statistic is then the average of 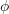 evaluated at all
evaluated at all 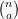 distinct combinations of
distinct combinations of 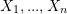 ,
,
![Rendered by QuickLaTeX.com \[U_n = \frac{1}{{n \choose a}} \mathop{\sum … \sum} \limits_{1 \leq i_1 < ... < i_a \leq n} \phi(X_{i_1}, ..., X_{i_a}).\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-728815bae7bbefe9378c01133409cdec_l3.png)
While 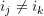 within each summand now, each
within each summand now, each 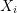 still appears in multiple summands, suggesting that
still appears in multiple summands, suggesting that 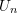 is the sum of correlated terms. As a result, the central limit theorem cannot be relied upon to determine the limiting distribution of
is the sum of correlated terms. As a result, the central limit theorem cannot be relied upon to determine the limiting distribution of 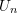 .
.
For more details on expectation functionals and their estimators, you can check out my blog post U-, V-, and Dupree statistics!
This blog post provides a walk-through derivation of the limiting, or asymptotic, distribution of a single U-statistic 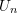 .
.
Continue reading Getting to know U: the asymptotic distribution of a single U-statistic



![Rendered by QuickLaTeX.com \[\text{Var}_{F}~ U_n = \frac{1}{{n \choose a}^2} \mathop{\sum \sum} \limits_{\substack{1 \leq i_1 < ... < i_{a} \leq n \\ 1 \leq j_1 < ... < j_{a} \leq n}} \text{Cov}\left[\phi(X_{i_1}, ..., X_{i_a}),~ \phi(X_{j_1}, ..., X_{j_a})\right].\]](https://statisticelle.com/wp-content/ql-cache/quicklatex.com-a2c21d5d7f01714fd65d97bc9e5366a0_l3.png)