Introduction

At the end of my latest blog post, I promised that I would talk about how to perform constrained maximization using unconstrained optimizers. This can be accomplished by employing clever transformation and nice properties of maximum likelihood estimators – see this fantastic post from the now defunct 🙁 Econometrics Beat. Eventually I will get around to discussing more of the statistical details behind this approach and its implementation from scratch in R.

RIGHT NOW, I want to talk about how to obtain standard errors for Gaussian mixture model parameters estimated using the EM algorithm. So far, I’ve written two posts with respect to Gaussian mixtures and the EM algorithm:

1. Embracing the EM algorithm: One continuous response, which motivates the theory behind the EM algorithm using a two component Gaussian mixture model; and
2. EM Algorithm Essentials: Maximizing objective functions using R’s optim, which demonstrates how to implement log-likelihood maximization from scratch using the optim function.

Both posts so far have focused only on POINT ESTIMATION! That is, obtaining estimates of our mixture model parameters.

Any estimate we obtain using any statistical method has some uncertainty associated with it. We quantify the uncertainty of a parameter estimate by its STANDARD ERROR. If we repeated the same experiment with comparable samples a large number of times, the standard error would reflect how much our estimates differ from experiment to experiment. Indeed, we would estimate the standard error as the standard deviation of the effect estimates across experiments. If we can understand how our estimates vary across experiments, i.e., estimate their standard errors, we can perform statistical inference by testing hypotheses or constructing confidence intervals, for example.

We usually do not need to conduct all of these experiments because theory tells us what form this distribution of effect estimates takes! We refer to this distribution as the SAMPLING DISTRIBUTION. When the form of the sampling distribution is not obvious, we may use resampling techniques to estimate standard errors. The EM algorithm, however, attempts to obtain maximum likelihood estimates (MLEs) which have theoretical sampling distributions. For well-behaved densities, MLEs can be shown to be asymptotically normally distributed and unbiased with a variance-covariance matrix equal to the inverse of the Fisher Information matrix, i.e., a function of the second derivatives of the log-likelihood or equivalently, the square of the first derivatives…

The tricky bit with the EM algorithm is we don’t maximize the observed log-likelihood directly to estimate Gaussian mixture parameters. Instead, we maximize a more convenient objective function. People much smarter than I have figured out this can give you the same answer. A question remains: if standard errors are estimated using the second derivative of the log-likelihood, but we used the objective function, how do we properly quantify uncertainty? Particularly as the derivatives of the log-likelihood are not straight-forward, for the same reasons that make optimization difficult.

Isaac Meilijson, another person smarter than me, provides us with a wealth of guidance in his 1989 paper titled A Fast Improvement to the EM Algorithm on its Own Terms (I love this title). In this blog post, we summarize and demonstrate how to construct simple estimators of the observed information matrix, and subsequently the standard errors of our EM estimates, when we have independent and identically distributed responses arising from a two-component Gaussian mixture model. Essentially, due to some nice properties, we can simply use the derivatives of our objective function, in lieu of our log-likelihood, to estimate the observed information. Standard errors computed using the observed information are then compared to those obtained using numerical differentiation of the observed log-likelihood.

Review

Fisher information

Consider random variables which are independent and identically distributed (i.i.d.) according to some density with parameters, . Let represent the observed values or realization of .

We wish to estimate using maximum likelihood estimation. Because the are i.i.d., the likelihood (equal to the joint density of ) is defined as,

   

We desire the estimates which maximize this likelihood,

   

That is, we seek the parameter values which make the observed most likely. Rather than maximizing the likelihood directly, it is convenient to instead maximize the log-likelihood, particularly because many common , including the normal, Bernoulli, Poisson, and exponential distributions, belong to the exponential family. The log-likelihood is thus,

   

Maximizing the log-likelihood with respect to is equivalent to solving the equations,

   

which yields the maximum likelihood estimates .

When certain conditions are met (they are for the following examples), asymptotically where is the inverse of the expected Fisher information matrix. The expected Fisher information matrix can be expressed as,

   

or the negative expected value of the second derivative of the log-likelihood. If the second derivative of the log-likelihood is small when evaluated at , it suggests the likelihood is flat in the region of the MLE, or that there is lots of uncertainty with respect to . Thus, will be large. Often times, the observed Fisher information is used for variance estimation instead,

   

as it avoids the need to take the expectation.

The vector of first derivatives can be re-expressed as,

   

and is referred to as the score function. The score function has very interesting, and convenient properties:

1. The expected value of the score function is zero: ;
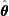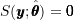2. When evaluated at the MLE , the score function is equal to by definition: ; and
3. The variance of the score function is the Fisher information: .

This suggests a third form of the Fisher information matrix, referred to as the empirical Fisher information matrix,

   

or equivalently, because the individual score components are also i.i.d., :

   

When evaluated at the MLE , this simplifies to,

   

We can then invert the empirical Fisher information matrix at to estimate the covariance of the MLE estimates, . This is a nice result because it means we only need to compute the first derivatives of the log-likelihood. First derivatives can be challenging, let alone higher order derivatives.

Objective function for two-component mixture model

Suppose that is a vector of i.i.d. random variables following a two-component Gaussian mixture with mixing probability and density,

   

where corresponds to the Normal density of subpopulation with mean and variance . Let represent the realization of and represent the vector of all parameters. The observed log-likelihood is then,

   

For reasons previously explained elsewhere, mixture log-likelihoods can be challenging to maximize. Instead, we use the EM algorithm to iteratively maximize the objective function,

   

where parameter estimates at iteration are obtained as,

   

using fixed weights,

   

That is, the EM algorithm solves,

   

at iteration , rather than . If then . Thus, increasing will increase , though there is no guarantee that maximizing Q will yield the MLE.

Standard errors for EM estimates

No matter! The results of Louis (1982), summarized in Meilijson (1989), tell us that for any , where,

   

This result also holds for a single such that, . This means that for EM estimates , we can estimate the empirical information matrix using the “objective score function” rather than the score function :

   

or equivalently, . Awesome, let’s test this out!

“Objective score function” for Gaussian mixture

For notational simplicity, let:

   

where represents the element or summand of the objective function. Then, the elements of are:

   

   

   

   

   

In this case, it is easy to check that with some additional work. For example,

   

P.S. you can see how the second derivative of the observed log-likelihood may get really nasty really quick.

Empirical information for simulated data

Data generation

Here, we apply the empirical information estimator to data generated in the same way as Embracing the EM algorithm: One continuous response. The true vector of parameters is .

set.seed(12345)

# Simulate two-component Gaussian mixture
## Sample size
N = 5000
## Parameters for first component
mu1 <- 5; var1 <- 1
## Parameters for second component
mu2 <- 2; var2 <- 1.25^2
## Mixing probability
pi <- 0.6
## True parameter vector
truth <- c(pi, mu1, var1, mu2, var2)

## Sample latent class
z <- rbinom(n=N, size=1, prob=pi)
## Sample response based on latent class
y1 <- rnorm(n=sum(z==1), mean=mu1, sd=sqrt(var1))
y2 <- rnorm(n=sum(z==0), mean=mu2, sd=sqrt(var2))
# Combine all responses into a single vector
y  <- c(y1, y2)

EM estimation

EM estimates are obtained by following EM Algorithm Essentials: Maximizing objective functions using R’s optim… The only difference being that we perform an additional E-step using the final EM estimates to update the weights.

# First density
f1 <- function(y, Mu1, Var1, log=F){ dnorm(y, mean=Mu1, sd=sqrt(Var1), log=log) }

# Second density
f2 <- function(y, Mu2, Var2, log=F){ dnorm(y, mean=Mu2, sd=sqrt(Var2), log=log) }

EStep <- function(y, theta){
  # E-STEP: Estimate weights
  # Extract parameter values
  Pi  <- theta[1]
  Mu1 <- theta[2]; Var1 <- theta[3]
  Mu2 <- theta[4]; Var2 <- theta[5]
  
  # Compute numerator and denominator of weight w
  Numerator <- Pi * f1(y, Mu1, Var1)
  Denominator <- Pi * f1(y, Mu1, Var1) + (1-Pi) * f2(y, Mu2, Var2)
  
  # Calculate and return weights W
  w <- Numerator / Denominator
  return(w)
}

Q <- function(y, w, theta){
  # OBJECTIVE FUNCTION
  
  # Extract parameter values
  Pi  <- theta[1]
  Mu1 <- theta[2]; Var1 <- theta[3]
  Mu2 <- theta[4]; Var2 <- theta[5]
  
  # Calculate two terms of Q per subject (notice log=T in f)
  Term1 <- w*log(Pi) + w*f1(y, Mu1, Var1, log=T)
  Term2 <- (1-w)*log(1-Pi) + (1-w)*f2(y, Mu2, Var2, log=T)
  
  # Add 'em all together and return
  Q <- sum(Term1) + sum(Term2)
  return(Q)
}

MStep <- function(y, w, theta){
  # M-STEP: Maximize objective function
  # Specify optim arguments
  maxQ <- optim(# function to optimize
                fn = Q,
                # initial (current) parameter values
                par = theta,
                # additional user specified arguments to pass to fn
                y = y,
                w = w,
                # optimization method, see help for options
                method = 'BFGS',
                # optim minimizes by default, specify fnscale = -1 to maximize
                control = list(fnscale = -1)
  )
  
  # Return results of maximization = (Q, theta)
  results <- list(Qval=maxQ$value, theta=maxQ$par)
}

Q_vec <- c()
est_list <- list()

for (b in 1:1000){
  
  # Initialize parameter values 
  if (b==1){     
    # Apply k-means with two centers
    kinit <- kmeans(y, centers=2)
    # Store predicted cluster labels
    cluster <- kinit$cluster
    
    # Estimate mixture probability
    Pi <- sum(cluster==1)/N
    # Estimate first component parameters
    y1 <- y[cluster==1]
    Mu1 <- mean(y1)
    Var1 <- var(y1)
    # Estimate second component parameters
    y2 <- y[cluster==2]
    Mu2 <- mean(y2)
    Var2 <- var(y2)
    # Parameter vector
    theta <- c(Pi, Mu1, Var1, Mu2, Var2)
    # Objective function
    Qval <- Q(y, EStep(y, theta), theta)
  } 
  
  else { 
    # E-Step
    w <- EStep(y, theta)
    # M-Step
    M <- MStep(y, w, theta)
    Qval <- M$Qval 
    theta <- M$theta
  }
  
  # Update log-likelihood vector and estimate list
  Q_vec[b] <- Qval
  est_list[[b]] <- theta 
  
  if (b > 1) { if (abs(Q_vec[b] - Q_vec[(b-1)]) < 0.01) break }
}

# Final estimates of Theta
ThetaEM <- est_list[[length(Q_vec)]]

The final estimates were 0.41, 2, 1.64, 5, 0.96 which align closely with the true Theta = 0.6, 5, 1, 2, 1.5625, but with labels reversed. Here, we fix the labels, and re-estimate the weights using Theta.

Theta <- c('Pi'=1-ThetaEM[1], 'Mu1'=ThetaEM[4], 'Var1'=ThetaEM[5], 'Mu2'=ThetaEM[2], 'Var2'=ThetaEM[3])
w <- EStep(y, Theta)

As a result, we have: = 0.59, 5, 0.96, 2, 1.64.

Empirical information and standard errors

Now, we define functions corresponding to the elements of the “objective score function” . Remember: to obtain the empirical information matrix, we estimate the variance of the individual objective score vectors. Thus, we need the value of for each individual. The following code returns 5 columns for each individual corresponding to their objective score vectors of length .

# Derivative of Q w.r.t Pi
dQi_Pi   <- function(wi, yi, Theta){ wi/Theta['Pi'] - (1-wi)/(1-Theta['Pi'])}

# Derivative of Q for first component parameters
dQi_Mu1  <- function(wi, yi, Theta){ wi*(yi-Theta['Mu1'])/Theta['Var1'] }
dQi_Var1 <- function(wi, yi, Theta){ wi*((yi - Theta['Mu1'])^2 - Theta['Var1'])/(2*Theta['Var1']^2)}

# Derivative of Q for second component parameters
dQi_Mu2  <- function(wi, yi, Theta){ (1-wi)*(yi-Theta['Mu2'])/Theta['Var2'] }
dQi_Var2 <- function(wi, yi, Theta){ (1-wi)*((yi-Theta['Mu2'])^2 - Theta['Var2'])/(2*Theta['Var2']^2)}

# Store all results with one row vector per individual
dQi_vec <- function(wi, yi, Theta){
  dQi <- cbind(dQi_Pi(wi, yi, Theta), 
               dQi_Mu1(wi, yi, Theta), 
               dQi_Var1(wi, yi, Theta),
               dQi_Mu2(wi, yi, Theta), 
               dQi_Var2(wi, yi, Theta))
  colnames(dQi) <- paste0('d',names(Theta))
  return(dQi)
}

# Calculate objective score components, and print a sample
dQi <- dQi_vec(w,y,Theta)
head(dQi)

##             dPi       dMu1       dVar1       dMu2      dVar2
## [1,] 0.95027906 -0.7872663 -0.05291849 0.22518904 0.08927032
## [2,] 1.63465475  0.6178672 -0.32241758 0.02620293 0.02514214
## [3,] 1.59079522  0.2134612 -0.48677399 0.04408917 0.03631870
## [4,] 0.06442835 -0.8809340  0.31884283 0.38535047 0.07091540
## [5,] 1.08828061 -0.7185802 -0.14532087 0.19270057 0.08536470
## [6,] 1.62744436  0.5275321 -0.37362115 0.02930063 0.02723943

Next, we estimate by multiplying the sample size by the estimated variance of the objective score components . The variance-covariance matrix of is obtained by inverting using the solve function. Taking the square root of the diagonal of the variance-covariance matrix gives us the standard errors for each element of .

H <- N*var(dQi)
rownames(H) <- colnames(H) <- names(Theta)
EmpVar <- solve(H)
EmpSE <- sqrt(diag(EmpVar))

## H:
H

##              Pi        Mu1       Var1        Mu2       Var2
## Pi   15291.9181 1731.67519 -895.24744 1391.26330  486.43460
## Mu1   1731.6752 2336.78831  547.37106 -319.38856  -16.21773
## Var1  -895.2474  547.37106 1035.94009   79.56311  -58.43365
## Mu2   1391.2633 -319.38856   79.56311  811.46535 -215.95742
## Var2   486.4346  -16.21773  -58.43365 -215.95742  246.26277

## Variance-covariance matrix:
EmpVar

##                 Pi           Mu1          Var1          Mu2         Var2
## Pi    0.0003675139 -0.0006374766  0.0006594684 -0.001445827 -0.001879341
## Mu1  -0.0006374766  0.0016459897 -0.0014395852  0.002811064  0.003491127
## Var1  0.0006594684 -0.0014395852  0.0023248343 -0.002804938 -0.003305549
## Mu2  -0.0014458268  0.0028110637 -0.0028049383  0.007467666  0.008924143
## Var2 -0.0018793411  0.0034911274 -0.0033055495  0.008924143  0.015044395

## Standard errors:
EmpSE

##         Pi        Mu1       Var1        Mu2       Var2 
## 0.01917065 0.04057080 0.04821654 0.08641566 0.12265559

Putting our point estimates and their standard errors based on the empirical information matrix side by side, we have:

cbind(Theta, EmpSE)

##          Theta      EmpSE
## Pi   0.5937860 0.01917065
## Mu1  5.0046047 0.04057080
## Var1 0.9581729 0.04821654
## Mu2  2.0020342 0.08641566
## Var2 1.6396322 0.12265559

Comparison to numerical differentiation

Apparently the empirical information has a subpar reputation?? The realistic alternative to using the empirical information matrix is to use numerical differentiation to compute the Hessian of the observed log-likelihood, and then multiply that by -1 to approximate the observed Fisher information. Let’s use the hessian function within the numDeriv library to do just that, and compare!

library(numDeriv)

Here, we specify a function for the observed log-likelihood.

obsLL <- function(Theta, y){
  #' Observed log-likelihood
  summand <- log(Theta['Pi'] * f1(y, Theta['Mu1'], Theta['Var1']) +
                   (1-Theta['Pi']) * f2(y, Theta['Mu2'], Theta['Var2']))
  LL <- sum(summand)
  return(LL)
}

Next, we use hessian to obtain the second derivative of the observed log-likelihood. Again, taking the inverse of the hessian gives us the variance-covariance matrix, and our SEs are equal to the square root of the diagonal.

estSE <- function(y, Theta){
  Hess <- hessian(func=function(Theta, y) obsLL(Theta, y), x=Theta, y=y)
  colnames(Hess) <- rownames(Hess) <- names(Theta)
  Var  <- solve(-Hess)
  SE   <- sqrt(diag(Var))
  return(list('Hessian'=Hess, 'Var'=Var, 'SE'=SE))
}

Applying this to our data and estimates, we get very similar results to before:

numResults <- estSE(y, Theta)
numResults

## $Hessian
##               Pi         Mu1        Var1         Mu2       Var2
## Pi   -15288.8597 -1731.18348   894.96393 -1391.41293 -487.01278
## Mu1   -1731.1835 -2336.44501  -540.42459   319.32468   16.21448
## Var1    894.9639  -540.42459 -1074.39207   -79.54719   58.42197
## Mu2   -1391.4129   319.32468   -79.54719  -810.75429  205.53416
## Var2   -487.0128    16.21448    58.42197   205.53416 -233.31043
## 
## $Var
##                 Pi           Mu1          Var1          Mu2         Var2
## Pi    0.0003406151 -0.0005777326  0.0005757352 -0.001316482 -0.001766736
## Mu1  -0.0005777326  0.0015142485 -0.0012547940  0.002528440  0.003224413
## Var1  0.0005757352 -0.0012547940  0.0020627894 -0.002421239 -0.002905448
## Mu2  -0.0013164817  0.0025284404 -0.0024212392  0.006841598  0.008344544
## Var2 -0.0017667358  0.0032244133 -0.0029054483  0.008344544  0.014821678
## 
## $SE
##         Pi        Mu1       Var1        Mu2       Var2 
## 0.01845576 0.03891335 0.04541794 0.08271395 0.12174431

and putting everything side-by-side we have:

cbind(Theta, EmpSE, 'NumSE'=numResults$SE)

##          Theta      EmpSE      NumSE
## Pi   0.5937860 0.01917065 0.01845576
## Mu1  5.0046047 0.04057080 0.03891335
## Var1 0.9581729 0.04821654 0.04541794
## Mu2  2.0020342 0.08641566 0.08271395
## Var2 1.6396322 0.12265559 0.12174431

In this case at least, results are very similar between the two approaches! The empirical SEs are slightly larger than the numerical SEs, so will result in slightly more conservative inference if anything.

Conclusion

In this blog post, we reviewed variance estimation for maximum likelihood estimates based on inversion of the Fisher information matrix. We then used properties of the score function and the EM objective function to derive the form of the empirical information matrix for EM estimates. Results were applied to a simulated dataset generated from a two-component Gaussian mixture model. Empirical standard errors were then compared to those obtain through numerical differentiation of the observed log-likelihood. Standard errors were similar between the two methods, with empirical standard errors being slightly larger than their numerical counterparts.

I think that the empirical information matrix approach to estimating SEs is really elegant in the i.i.d. case, requiring only the first derivatives of the objective function. The objective function is much easier to differentiate than the observed log-likelihood, with results providing the same values as the score function. These days, numerical differentiation is really easy to implement (one function definition + one line of code here) so why not! But what I take away from this is that the empirical information matrix can serve as a good sanity check for your numerical results.

Thanks for reading!