Motivation
For observed pairs ![]() ,
, ![]() , the relationship between
, the relationship between ![]() and
and ![]() can be defined generally as
can be defined generally as
![]()
where ![]() and
and ![]() . If we are unsure about the form of
. If we are unsure about the form of ![]() , our objective may be to estimate
, our objective may be to estimate ![]() without making too many assumptions about its shape. In other words, we aim to “let the data speak for itself”.
without making too many assumptions about its shape. In other words, we aim to “let the data speak for itself”.
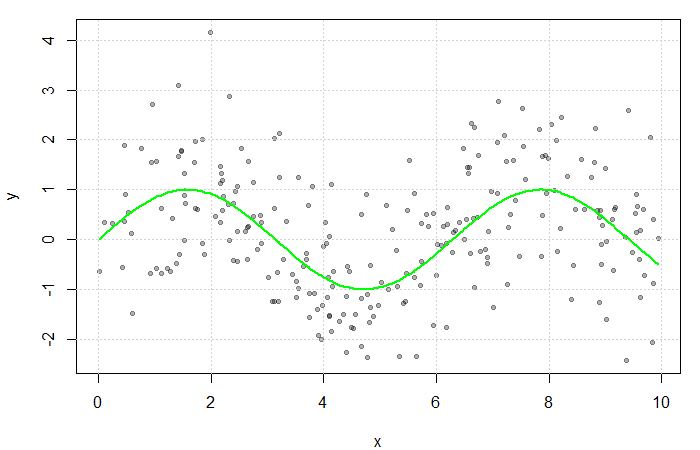
Simulated scatterplot of ![]() . Here,
. Here, ![]() and
and ![]() . The true function
. The true function ![]() is displayed in green.
is displayed in green.
Non-parametric approaches require only that ![]() be smooth and continuous. These assumptions are far less restrictive than alternative parametric approaches, thereby increasing the number of potential fits and providing additional flexibility. This makes non-parametric models particularly appealing when prior knowledge about
be smooth and continuous. These assumptions are far less restrictive than alternative parametric approaches, thereby increasing the number of potential fits and providing additional flexibility. This makes non-parametric models particularly appealing when prior knowledge about ![]() ‘s functional form is limited.
‘s functional form is limited.
Estimating the Regression Function
If multiple values of ![]() were observed at each
were observed at each ![]() ,
, ![]() could be estimated by averaging the value of the response at each
could be estimated by averaging the value of the response at each ![]() . However, since
. However, since ![]() is often continuous, it can take on a wide range of values making this quite rare. Instead, a neighbourhood of
is often continuous, it can take on a wide range of values making this quite rare. Instead, a neighbourhood of ![]() is considered.
is considered.
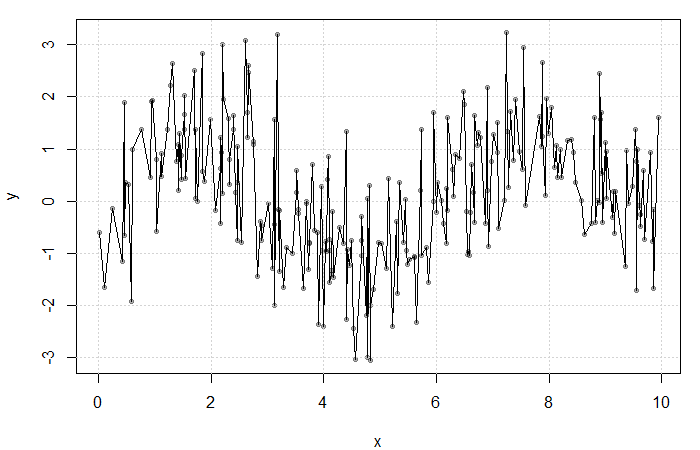
Result of averaging ![]() at each
at each ![]() . The fit is extremely rough due to gaps in
. The fit is extremely rough due to gaps in ![]() and low
and low ![]() frequency at each
frequency at each ![]() .
.
Define the neighbourhood around ![]() as
as ![]() for some bandwidth
for some bandwidth ![]() . Then, a simple non-parametric estimate of
. Then, a simple non-parametric estimate of ![]() can be constructed as average of the
can be constructed as average of the ![]() ‘s corresponding to the
‘s corresponding to the ![]() within this neighbourhood. That is,
within this neighbourhood. That is,
(1) ![]()
where
![]()
is the uniform kernel. This estimator, referred to as the Nadaraya-Watson estimator, can be generalized to any kernel function ![]() (see my previous blog bost). It is, however, convention to use kernel functions of degree
(see my previous blog bost). It is, however, convention to use kernel functions of degree ![]() (e.g. the Gaussian and Epanechnikov kernels).
(e.g. the Gaussian and Epanechnikov kernels).
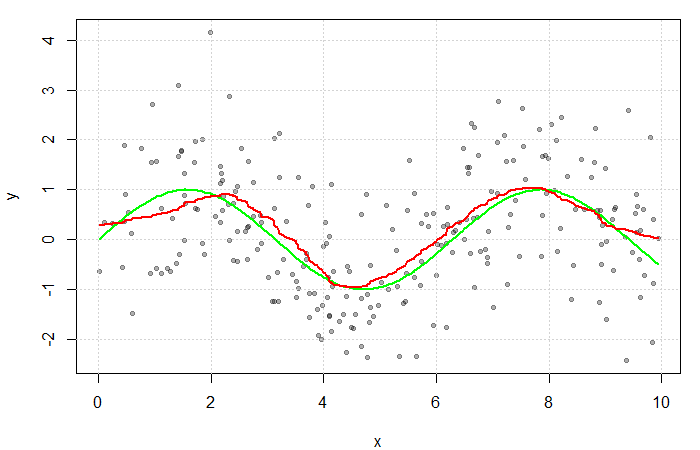
The red line is the result of estimating ![]() with a Gaussian kernel and arbitrarily selected bandwidth of
with a Gaussian kernel and arbitrarily selected bandwidth of ![]() . The green line represents the true function
. The green line represents the true function ![]() .
.
